Эйлеров Квадрат разгадать Eulero online
Эйлеров Квадрат или Греко-латинский квадрат - это увлекательный пример чего-то, что появилось сначала как загадка, затем как математическое любопытство без каких-либо практических целей и в итоге оказалось очень полезным для реальных проблем.
Уже в 1725 году греко-латинские квадраты существовали как головоломка с игральными картами. Головоломка, которую вы можете сыграть в своем браузере, нажав на ссылку с изображением справа, просто устроит 16 карточек лиц (включая тузы), так что каждая строка и столбец содержит только по одному значению и по одной масти (И в этой головоломке, но не в греко-латинских квадратах, две большие диагонали также должны иметь только одно из каждого значения и одно в каждой масти). Даже эта простая проблема сложнее, чем кажется.
Математик Леонард Эйлер назвал эти массивы греко-латинскими квадратами, поскольку он использовал буквы из греческого и латинского алфавитов для значений. Латинский квадрат имеет только одно «измерение», которое представлено буквами латинского алфавита (хотя есть три переменные: строки, столбцы и буквы). Простейшая форма - квадрат 3 3, в котором буквы A, B и C появляются один раз в каждой строке и один раз в каждом столбце.
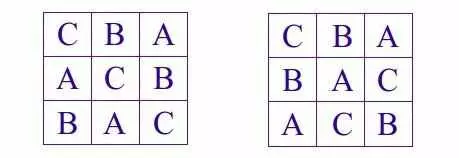
Квадраты выше являются латинскими квадратами порядка 3. Правая находится в ее приведенной или нормированной форме, потому что и первая строка, и первый столбец находятся в их естественном порядке. Вы можете видеть, что латинские квадраты не сложны для создания, и число возможных перестановок увеличивается с размером квадрата.
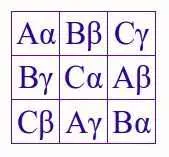
Чтобы создать греко-латинский квадрат, мы добавляем второе измерение, накладывая квадрат греческими буквами на латинский квадрат. Два квадрата должны быть взаимно ортогональными, то есть каждая греко-латинская пара встречается только один раз. Поэтому тот же квадрат не может быть наложен на себя, но мы можем использовать два латинских квадрата сверху, переключить один на греческий и наложить его над другим, чтобы достичь этого греко-латинского квадрата порядка 3. Греко-латинские квадраты Также называемые взаимно ортогональными латинскими квадратами.
Эйлер посвятил исследование этих механизмов в 18 веке. Он отметил, что нет греко-латинского квадрата второго порядка, и он не мог построить один из 6-го порядка - проблему, которую он поставил в качестве Тридцать шестой задачи сотрудников. Он предположил, что греко-латинские квадраты не существуют для любого порядка n, где n - четное число, не делящееся на 4, но в 1959 году математики смогли опровергнуть эту гипотезу. Они обнаружили греко-латинские квадраты порядка 10 и доказали, что они существуют для каждого порядка, кроме 2 и 6.
Практическое использование
Греко-латинские квадраты полезны для разработки научных экспериментов и эффективной организации турниров.
Graeco-Latin Sudoku - интересная вариация судоку, которую вы могли бы поспорить, дает вам в два раза удовольствие от обычной головоломки судоку!
Этот сайт содержит много головоломок Греко-латинский квадрат разных размеров и трудностей. Мы протестировали диапазон размеров и считаем, что этот размер 5х5 наиболее интересен для этого конкретного варианта.
Значит, у него странное имя - что это? Хорошо, латинский квадрат, который большинство из нас знакомо, и содержит ряд чисел один раз в каждой строке и столбце. Квадрат Graeco содержит ряд букв таким же образом. Поэтому, если вы соедините их, вы получите греко-латинский квадрат: то есть тот, который содержит букву один раз в каждой строке / столбце И число тоже.
Поэтому правила должны помещать каждый из 1 - 5 и A - E один раз в каждую строку и столбец. Кроме того, каждая из 25 комбинаций от A1 до E5 также появляется один раз во всей головоломке. Это добавляет интересный поворот в логику решения и в то же время означает, что 5x5 - о правильном размере, так как вы не хотите тратить свою жизнь на сохранение и регистрацию 81 возможных комбинаций, чтобы сократить, как это было бы с кропотливым случаем с 9x9 Версия этой головоломки! Но наличие 25, как в головоломке 5x5, кажется правильным.
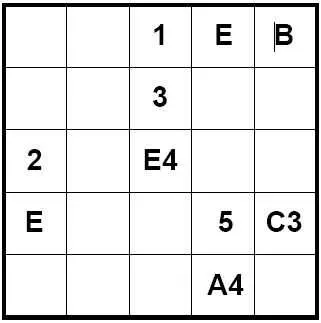
Если вы когда-либо застреваете во время решения этих головоломок, вы, вероятно, пропустили приложение интересной логики, вытекающей из этого правила уникальности. Посмотрите на образец головоломки справа. Третья ячейка содержит 'E', но какое число она содержит? Ну, это не может быть 1 или 5 из строки / столбца, но также E4 уже помещен в сетку, так что он не может быть равным 4. Это должно быть 2 или 3 поэтому. Часто вы обнаружите, что есть только одна ячейка, которая может иметь конкретную комбинацию, и поэтому вы можете поместить ее туда. По мере того, как вы полностью решаете число и букву в ячейке, хорошая практика заключается в том, чтобы пройти через какие-то неполные ячейки и тут же произвести любые возможные исключения.
Почему бы вам не пойти на образец страницы Graeco Latin Sudoku и посмотреть, нравится вам этот тип головоломки или нет: если вы это сделаете, вы можете разгадать онлайн, содержащий много головоломок из этого нового раздела выше.
Инструкции Квадрат Эйлера:
Вот как играть в греко-латинский судоку:
Греко-латинское судоку требует, чтобы вы указывали числа 1 - n и буквы A - n ровно один раз в каждой строке и столбце сетки.
Например, с головоломкой 5 x 5 буквы A, B, C, D, E и цифры 1, 2, 3, 4, 5 должны размещаться ровно один раз в каждой строке и столбце. Каждая ячейка содержит как букву, так и цифру.
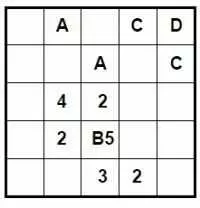
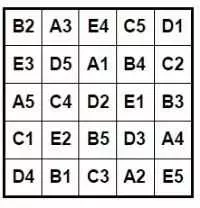
Кроме того, каждая ячейка должна содержать уникальную комбинацию. Таким образом, если ячейка содержит «B5», то никакая другая ячейка в загадке не может содержать «B5».
Большинство людей никогда не столкнутся с греко-латинским судоку. Причина этого в том, что он редко встречается в печати.
Хотя концепция наличия одного значения в каждой ячейке в значительной степени священа с судоку, это правило нарушено здесь, и в каждой ячейке есть число и буква.
Тем не менее, для тех, у кого есть опытные решатели судоку, это не будет слишком сильным толчком, и те же правила, что и для судоку, могут применяться к буквам и цифрам индивидуально, и некоторый прогресс может быть достигнут таким путем.
Чтобы решить эти головоломки, вам непременно нужно будет обратить внимание на то, что каждая комбинация букв и цифр уникальна, поэтому с головоломкой 5х5 25 комбинаций от А1 до Е5 появляются ровно один раз.
Этот факт вносит некоторую приятную логику, на простейшем уровне, уже размещенную «B1» и имеющую четыре другие ячейки, которые содержат «B», но вы понятия не имеете об их значении, тогда вы можете исключить «1» как опцию из Каждая из этих ячеек, поскольку эта комбинация уже помещена в сетку.
Греко-латинский квадрат иногда называют ABCDoku или Греко-латинское судоку.
Эти пазлы обычно публикуются с гораздо меньшим размером, чем 9х9, и 5х5 является наиболее распространенным. Это потому, что для того, чтобы отслеживать 81 уникальные комбинации, это может стать довольно утомительным, так что эти головоломки лучше всего подходят для размера 5х5.
Головоломка Эйлеров Квадрат 4x4
Уже в 1725 году греко-латинские квадраты существовали как головоломка с игральными картами. Головоломка, которую вы можете сыграть в своем браузере, нажав на ссылку с изображением справа, просто устроит 16 карточек лиц (включая тузы), так что каждая строка и столбец содержит только по одному значению и по одной масти (И в этой головоломке, но не в греко-латинских квадратах, две большие диагонали также должны иметь только одно из каждого значения и одно в каждой масти). Даже эта простая проблема сложнее, чем кажется.
Головоломка Латинские квадраты
Математик Леонард Эйлер назвал эти массивы греко-латинскими квадратами, поскольку он использовал буквы из греческого и латинского алфавитов для значений. Латинский квадрат имеет только одно «измерение», которое представлено буквами латинского алфавита (хотя есть три переменные: строки, столбцы и буквы). Простейшая форма - квадрат 3 3, в котором буквы A, B и C появляются один раз в каждой строке и один раз в каждом столбце.

Квадраты выше являются латинскими квадратами порядка 3. Правая находится в ее приведенной или нормированной форме, потому что и первая строка, и первый столбец находятся в их естественном порядке. Вы можете видеть, что латинские квадраты не сложны для создания, и число возможных перестановок увеличивается с размером квадрата.
Эйлеров Квадрат разгадывать бесплатно

Чтобы создать греко-латинский квадрат, мы добавляем второе измерение, накладывая квадрат греческими буквами на латинский квадрат. Два квадрата должны быть взаимно ортогональными, то есть каждая греко-латинская пара встречается только один раз. Поэтому тот же квадрат не может быть наложен на себя, но мы можем использовать два латинских квадрата сверху, переключить один на греческий и наложить его над другим, чтобы достичь этого греко-латинского квадрата порядка 3. Греко-латинские квадраты Также называемые взаимно ортогональными латинскими квадратами.
Эйлер посвятил исследование этих механизмов в 18 веке. Он отметил, что нет греко-латинского квадрата второго порядка, и он не мог построить один из 6-го порядка - проблему, которую он поставил в качестве Тридцать шестой задачи сотрудников. Он предположил, что греко-латинские квадраты не существуют для любого порядка n, где n - четное число, не делящееся на 4, но в 1959 году математики смогли опровергнуть эту гипотезу. Они обнаружили греко-латинские квадраты порядка 10 и доказали, что они существуют для каждого порядка, кроме 2 и 6.
Практическое использование
Греко-латинские квадраты полезны для разработки научных экспериментов и эффективной организации турниров.
Graeco-Latin Sudoku - интересная вариация судоку, которую вы могли бы поспорить, дает вам в два раза удовольствие от обычной головоломки судоку!

Этот сайт содержит много головоломок Греко-латинский квадрат разных размеров и трудностей. Мы протестировали диапазон размеров и считаем, что этот размер 5х5 наиболее интересен для этого конкретного варианта.
Значит, у него странное имя - что это? Хорошо, латинский квадрат, который большинство из нас знакомо, и содержит ряд чисел один раз в каждой строке и столбце. Квадрат Graeco содержит ряд букв таким же образом. Поэтому, если вы соедините их, вы получите греко-латинский квадрат: то есть тот, который содержит букву один раз в каждой строке / столбце И число тоже.
Поэтому правила должны помещать каждый из 1 - 5 и A - E один раз в каждую строку и столбец. Кроме того, каждая из 25 комбинаций от A1 до E5 также появляется один раз во всей головоломке. Это добавляет интересный поворот в логику решения и в то же время означает, что 5x5 - о правильном размере, так как вы не хотите тратить свою жизнь на сохранение и регистрацию 81 возможных комбинаций, чтобы сократить, как это было бы с кропотливым случаем с 9x9 Версия этой головоломки! Но наличие 25, как в головоломке 5x5, кажется правильным.
Если вы когда-либо застреваете во время решения этих головоломок, вы, вероятно, пропустили приложение интересной логики, вытекающей из этого правила уникальности. Посмотрите на образец головоломки справа. Третья ячейка содержит 'E', но какое число она содержит? Ну, это не может быть 1 или 5 из строки / столбца, но также E4 уже помещен в сетку, так что он не может быть равным 4. Это должно быть 2 или 3 поэтому. Часто вы обнаружите, что есть только одна ячейка, которая может иметь конкретную комбинацию, и поэтому вы можете поместить ее туда. По мере того, как вы полностью решаете число и букву в ячейке, хорошая практика заключается в том, чтобы пройти через какие-то неполные ячейки и тут же произвести любые возможные исключения.
Почему бы вам не пойти на образец страницы Graeco Latin Sudoku и посмотреть, нравится вам этот тип головоломки или нет: если вы это сделаете, вы можете разгадать онлайн, содержащий много головоломок из этого нового раздела выше.
Греко-латинское судоку
Инструкции Квадрат Эйлера:
Вот как играть в греко-латинский судоку:
Греко-латинское судоку требует, чтобы вы указывали числа 1 - n и буквы A - n ровно один раз в каждой строке и столбце сетки.
Например, с головоломкой 5 x 5 буквы A, B, C, D, E и цифры 1, 2, 3, 4, 5 должны размещаться ровно один раз в каждой строке и столбце. Каждая ячейка содержит как букву, так и цифру.


Кроме того, каждая ячейка должна содержать уникальную комбинацию. Таким образом, если ячейка содержит «B5», то никакая другая ячейка в загадке не может содержать «B5».
Большинство людей никогда не столкнутся с греко-латинским судоку. Причина этого в том, что он редко встречается в печати.
Хотя концепция наличия одного значения в каждой ячейке в значительной степени священа с судоку, это правило нарушено здесь, и в каждой ячейке есть число и буква.
Тем не менее, для тех, у кого есть опытные решатели судоку, это не будет слишком сильным толчком, и те же правила, что и для судоку, могут применяться к буквам и цифрам индивидуально, и некоторый прогресс может быть достигнут таким путем.
Чтобы решить эти головоломки, вам непременно нужно будет обратить внимание на то, что каждая комбинация букв и цифр уникальна, поэтому с головоломкой 5х5 25 комбинаций от А1 до Е5 появляются ровно один раз.
Этот факт вносит некоторую приятную логику, на простейшем уровне, уже размещенную «B1» и имеющую четыре другие ячейки, которые содержат «B», но вы понятия не имеете об их значении, тогда вы можете исключить «1» как опцию из Каждая из этих ячеек, поскольку эта комбинация уже помещена в сетку.
Греко-латинский квадрат иногда называют ABCDoku или Греко-латинское судоку.
Эти пазлы обычно публикуются с гораздо меньшим размером, чем 9х9, и 5х5 является наиболее распространенным. Это потому, что для того, чтобы отслеживать 81 уникальные комбинации, это может стать довольно утомительным, так что эти головоломки лучше всего подходят для размера 5х5.
Петро Полюхович © 2011-2024
Приєднуйтесь до нас, якщо ви справжній поціновувач кросвордів!


 Ввійти
Ввійти Кросворди
Кросворди Головоломки
Головоломки Судоку
Судоку Англійські
Англійські Турецькі
Турецькі Про сайт
Про сайт