Как разгадывать Инь Ян (Yin-Yang)
Хотя большинство головоломок этого типа требуют, чтобы один цвет (обычно белый) был ортогонально смежным, для этого требуются оба цвета. Отсюда и название Инь Ян.
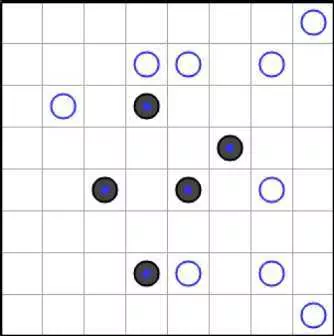
Неразрешенная головоломка состоит из квадратной сетки (размером 6х6, 8х8 или 10х10). Некоторые ячейки содержат белый или черный круг.
Цель Инь Ян состоит в том, чтобы заполнить все ячейки либо белым, либо черным кругом.
Решенная сетка головоломки должна удовлетворять следующим условиям:
Все белые клетки и все черные клетки должны образовывать ортогонально смежную область.
Все зоны 2x2 должны содержать по крайней мере один круг каждого цвета.
Как уже выше упоминалось в головоломке Инь-Ян нужно заполнить каждую ячейку черным кружком или белым кружком в соответствии со следующими правилами - Все ячейки с черными кружками образуют краевую область. Все ячейки с белыми кружками образуют краевую область. Нет квадрата 2x2 ячеек полностью заполнены кругами того же цвета.
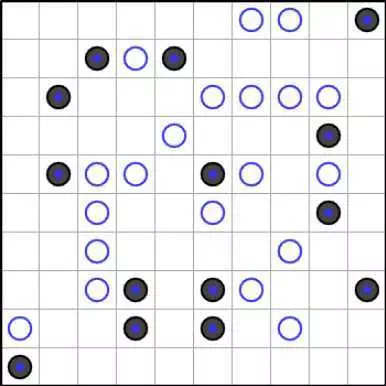
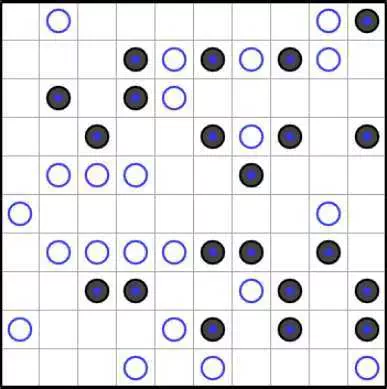
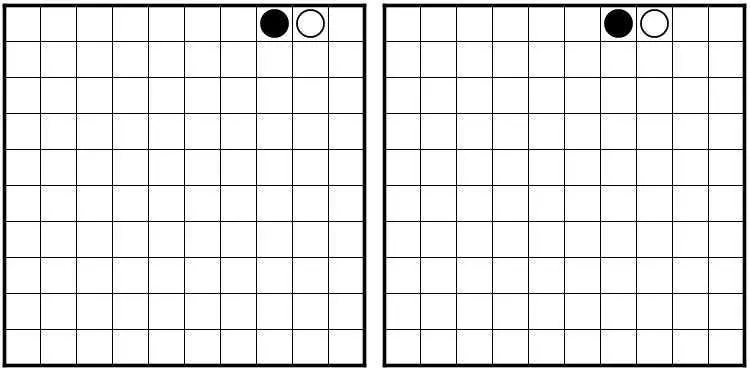
Ниже приведены две загадки «Инь-Янь». Какие из них, если они есть, имеют уникальное решение? (Естественно, дайте полное доказательство.)
Как заметил Гарет МакКоган, вне доски состоит из смежной группы белых квадратов и смежной группы черных квадратов; если на границе было более двух смежных белых групп, тогда было бы более двух черных групп, и путь, соединяющий белые группы, разделил бы черные группы.
Вызовите две вершины на границе, где белый встречается с черными A и B, где A - близкое к данному знаку. Представьте себе, начиная с точки A, и после границы черной области, пока вы не достигнете точки B.
Трассировка пути должна затрагивать каждую внутреннюю вершину хотя бы один раз. Если бы это не так, это означало бы, что в этой вершине не было изменения цвета, что означает, что он окружен твердым квадратом 2x2.
Путь не может дважды посещать внутреннюю вершину. Это означало бы, что квадрат 2x2 вокруг вершины был окрашен как шахматная доска. Но тогда путь, соединяющий противоположные белые квадраты, должен был бы отделить черные, поэтому этого не может произойти.
Поэтому граничный путь посещает каждую внутреннюю вершину ровно один раз.
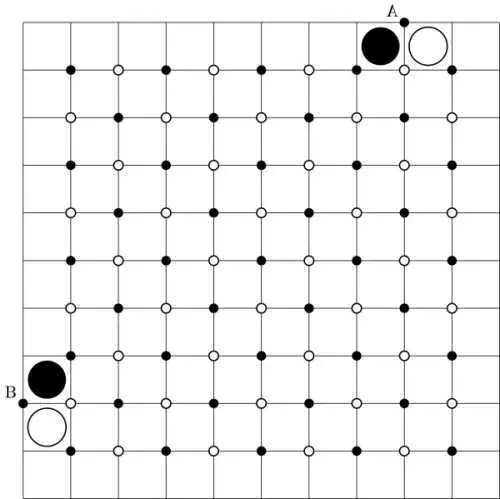
Здесь возникает противоречие. Покрасьте вершины этой сетки черным и белым в шахматном порядке, так что A черный. Граница должна чередоваться между черным и белым и посещает все 81 внутренние вершины плюс A и B для 83 вершин. Это означает, что он должен посетить 41 белый вершины, все в глубине. Но в интерьере всего 40 белых вершин! Поэтому эта головоломка не имеет решения.
Это также показывает, что решение левой головоломки задается любым гамильтоновым путем на внутренних вершинах, который начинается вблизи данных ключей и заканчивается у границы, из которых их много.
Цель головоломки Инь Ян (Yin Yang)
Неразрешенная головоломка состоит из квадратной сетки (размером 6х6, 8х8 или 10х10). Некоторые ячейки содержат белый или черный круг.
Цель Инь Ян состоит в том, чтобы заполнить все ячейки либо белым, либо черным кругом.
Правила Инь Ян:
Решенная сетка головоломки должна удовлетворять следующим условиям:
Все белые клетки и все черные клетки должны образовывать ортогонально смежную область.
Все зоны 2x2 должны содержать по крайней мере один круг каждого цвета.
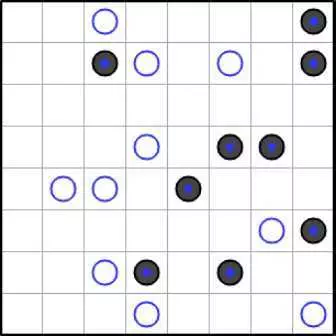
Пример решения головоломки Инь Ян
Как уже выше упоминалось в головоломке Инь-Ян нужно заполнить каждую ячейку черным кружком или белым кружком в соответствии со следующими правилами - Все ячейки с черными кружками образуют краевую область. Все ячейки с белыми кружками образуют краевую область. Нет квадрата 2x2 ячеек полностью заполнены кругами того же цвета.
Ниже приведены две загадки «Инь-Янь». Какие из них, если они есть, имеют уникальное решение? (Естественно, дайте полное доказательство.)
Начнем с рассмотрения самой головоломки.
Как заметил Гарет МакКоган, вне доски состоит из смежной группы белых квадратов и смежной группы черных квадратов; если на границе было более двух смежных белых групп, тогда было бы более двух черных групп, и путь, соединяющий белые группы, разделил бы черные группы.

Вызовите две вершины на границе, где белый встречается с черными A и B, где A - близкое к данному знаку. Представьте себе, начиная с точки A, и после границы черной области, пока вы не достигнете точки B.
Трассировка пути должна затрагивать каждую внутреннюю вершину хотя бы один раз. Если бы это не так, это означало бы, что в этой вершине не было изменения цвета, что означает, что он окружен твердым квадратом 2x2.
Путь не может дважды посещать внутреннюю вершину. Это означало бы, что квадрат 2x2 вокруг вершины был окрашен как шахматная доска. Но тогда путь, соединяющий противоположные белые квадраты, должен был бы отделить черные, поэтому этого не может произойти.
Поэтому граничный путь посещает каждую внутреннюю вершину ровно один раз.

Здесь возникает противоречие. Покрасьте вершины этой сетки черным и белым в шахматном порядке, так что A черный. Граница должна чередоваться между черным и белым и посещает все 81 внутренние вершины плюс A и B для 83 вершин. Это означает, что он должен посетить 41 белый вершины, все в глубине. Но в интерьере всего 40 белых вершин! Поэтому эта головоломка не имеет решения.
Это также показывает, что решение левой головоломки задается любым гамильтоновым путем на внутренних вершинах, который начинается вблизи данных ключей и заканчивается у границы, из которых их много.
Петро Полюхович © 2011-2024
Приєднуйтесь до нас, якщо ви справжній поціновувач кросвордів!


 Ввійти
Ввійти Кросворди
Кросворди Головоломки
Головоломки Судоку
Судоку Англійські
Англійські Турецькі
Турецькі Про сайт
Про сайт