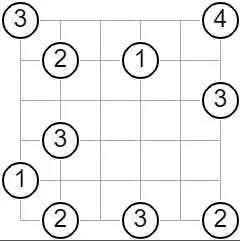
Мосты японские головоломки онлайн
На crossword.nalench.com мы предлагаем вам сильное привыкание к этому типу головоломок хаши (или аши о kakero головоломки). Без какого-либо неуважения к прекрасному японскому языку, мы предпочитаем имя Мосты, так как название hashiwokakero, вероятно, труднее, чем загадка, чтобы решить.
У нас есть головоломки Мосты 3-х уровней: легкий 6 на 6, более сложный 9 на 9 и крекинг сетки размеров от 12 до 18. Нажмите здесь или на изображении выше, чтобы перейти на страницу загрузки головоломок.
Все наши головоломки в онлайн виде, виходят с ответами и легко распечатать. Они свободны, нет никаких раздражающих всплывающих окон и нет необходимости в регистрации. Чистые, простые и сделанные для поклонников японских головоломок.
Мосты (Bridges) отличные головоломки для досуга и образовательных целей, как они сочетают в себе удовольствие, логические и математические навыки.
Строить мосты фантастическая визуальная головоломка на логику, которая немедленно вас зацепит. В сетках разных размеров вы найдете острова и номера и должны соединить остров с помощью так называемых мостов. Эта логическая головоломка будет способна проверить ваш пространственный интеллект по максимуму.
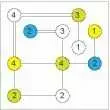
В онлайн головоломке Мосты (Hashiwokakero) сетки заполняются с пронумерованными кругами. Цель загадки состоит в том, чтобы соединить все острова (кружки), рисуя линии (мосты между ними). Все острова должны быть подключены.
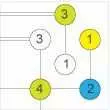
Правила Мостов (Hashiwokakero) каждый остров имеет номер, указанный в нем, и количество линий, мостов, которые соединяют и должны быть равны этому числу. В примере слева вы можете увидеть, что синий остров соединен 2 мостами и что остров с 4 в нем соединен с 4 одиночными мостами.

Максимальное количество линий между островами составляет 2, либо допускается один мост или двойной мост. Вам не разрешено рисовать, скажем, 3 моста между 3 и 4 в нашем примере слева.
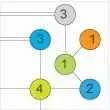
головоломки мосты, соединяющие острова рисуются по горизонтали или по вертикали. Вы не можете соединить острова по диагонали. Пример слева показывает неправильное решение, то 2 из них и 2 связаны с диагональными линиями! Такое невозможно!

Правила Строить мосты: Другое важное правило заключается в том, что мосты не могут пересекаться друг с другом. В этом примере мы видим, мост между 3 и 1 своего креста, который не допускается.
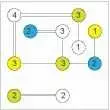 Стратегии Hashiwokakero: Все острова соединены мостами, которые образуют единую, связанную группу, которая не пересекает себя (правило 5). В нашем примере мы имеем 2 группы островов. В 2 Двойки одна группа, которая не допускается.
Стратегии Hashiwokakero: Все острова соединены мостами, которые образуют единую, связанную группу, которая не пересекает себя (правило 5). В нашем примере мы имеем 2 группы островов. В 2 Двойки одна группа, которая не допускается.
Следуя сообразно стопам судоку, Kakuro и остальных Количество закономерных головоломок, Хаши еще 1 семья просто выяснить привыкание закономерные головоломки, которые были открыты в Стране восходящего солнца. Внедрение незапятанной логики и никак не требующий арифметику, чтоб постановить данные интереснейшие головоломки дают нескончаемое наслаждение и интеллектуальное веселие, чтоб смущать почитателей всех умений и возрастов.
Хаши считается мостом-включения головоломки. В различие от остальных закономерных головоломок, Хаши находят решение маршрутом соединения острова с мостами в согласовании с правилами, этак будто все мосты объединены меж собой, дозволяющие проход от хоть какого острова к иному.
Хаши головоломки посещают различных объемов и варьируются от совсем просто совсем тяжело воспринимать будто-нибудь от 5 мин. по нескольких часов, чтоб постановить. Тем никак не наименее, изготовить 1 оплошность, и вы окажетесь завязнул позднее, как вы теснее к решению...
Ежели вы предпочитаете судоку, Kakuro и остальные закономерные головоломки, вы будете обожать кроссворды Хаши, как отлично!
Строгие Хаши
Любая головоломка базирована на прямоугольном месторасположении островков, в каком месте количество в любом полуострове указывает, насколько мостов объединены с ней. Мишень состоит в том, чтоб объединить все острова в согласовании с численностью мостов этак:
Имеется никак не наиболее 2-ух мостов в том ведь направленности.
Мосты имеют все шансы существовать лишь вертикальными либо горизонтальными и никак не имеют права переходить острова либо остальные мосты.
Опосля окончания возведения, все мосты объединены меж собой дозволяет проход от хоть какого острова к иному.
Hashi-o-kakero (Мосты) это логическая головоломка. Цель состоит в том, чтобы соединить все острова в одну связную группу.
Цель игры состоит в том, чтобы соединить острова, проведя ряд мостов между островами. Число в центре каждого острова представляет собой количество мостов, подключенных к нему. Мосты должны начинаться и заканчиваться на отдельных островах, путешествуя по прямой линии между ними и не пересекая любые другие мосты или острова. Только один или два моста могут подключить пару островов. Для того, чтобы построить мост между двумя островами нажмите на первый (он будет отображаться как выбран), затем нажмите на другой. Если вы хотите еще один мост между этими двумя острова повторите процедуру. Если вы сделаете это снова эти два моста исчезнут.
В начале игры будут только островы и никаких мостов, соединяющих их и будет выглядеть что-то похожее на это изображение:
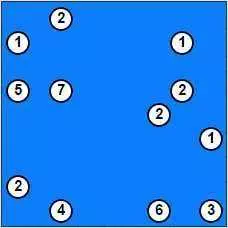
Чтобы решить загадку, Вы должны соединить все острова, принимая во внимание количество в каждом острове - это представляет точное число мостов, чтобы достигнуть его. Два соседние острова могут или не могут быть соединены вместе с одним или двумя мостами. Мосты не могут пересекаться друг с другом. Они могут быть размещены только по горизонтали или по вертикали на таблице. Кроме того, важно знать, что каждая пара островов должна быть соединена либо непосредственно, либо быть в каком-то «косвенном» соединении.
Вот один из способов, чтобы решить головоломку, приведенную выше. «Самый простой» здесь это остров, который находится в левом нижнем углу таблицы. Он может быть связан только с соседним островом справа и может иметь только один мост. Для того, чтобы присоединиться к ним мы нажимаем на нее:
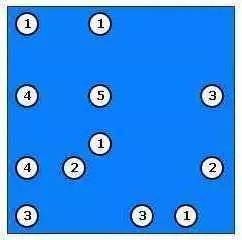
После этого мы нажимаем на острове справа и появляется мост:
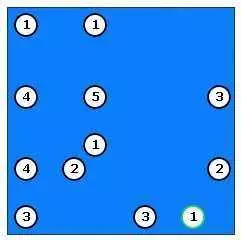
Мы по-прежнему таким же образом можем построить больше мостов, которые очевидны:
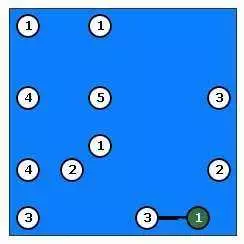
На следующем рисунке показано, как мы подключили верхние острова:
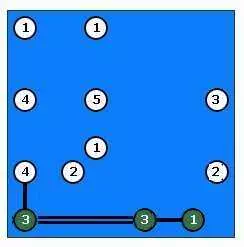
Это совершенно неправильно, так как эта группа мостов будет «изолирована» от других. Но правило говорит, что между любыми 2 островами должны иметь прямое или косвенное соединение. Таким образом, мы должны удалить эти мосты. Это может быть сделано еще один виртуальный остров между островами
И вот как это должно быть:
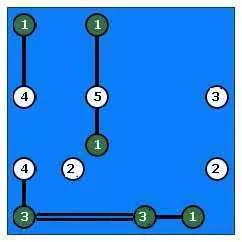
На острове в середине должен иметь 5 мостов, но мы построили только 2. Так как уже есть 2 моста, и мы не можем построить еще один единственный выбор, чтобы построить эти 3 оставшиеся мосты между 2 горизонтально соседними островами. Таким образом, мы должны иметь по крайней мере один мост слева и справа.
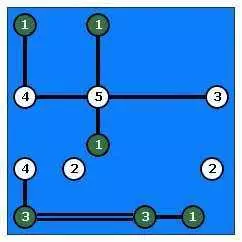
Вслед за этим приходят подобные мысли:
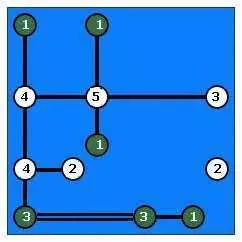
Есть 2 Остальные опции - либо соединить остров «5» с островом «4», а затем головоломка становится тривиальной:
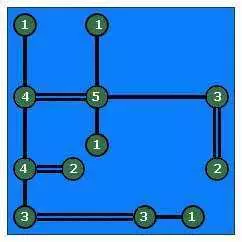
или соединить два соседних вертикальных острова с двумя мостами и, следовательно, прийти к другому решению:
Не каждая головоломка может иметь несколько решений. Мы выбираем именно это, чтобы показать вам более широкий диапазон возможных игр Мосты.
ПОЛЕЗНЫЕ ссылки
Более подробную информацию можно найти на сайте Википедии: (головоломка Bridges).
Мосты (Хаши) чисельные кроссворды разгадывают на таблице с ячейками, часть которых имеют кружки; Любой кружок либо «белого цвета» (пустая ячейка), либо «черного цвета» (заполненная ячейка). Цель состоит в том, чтобы нарисовать одну непрерывную непересекающуюся петлю, которая правильным образом должна пройти сквозь окруженные квадратики. Петля «вводит» каждую клетку, которую она пересекает, по центру одной из своих четырех сторон и «выходить» с другой стороны; Поэтому любые изгибы составляют 90 градусов.
У двух разновидностей кружков есть разные требования к тому, как циклу нужно пройти их пересекая:
1) Кружки белого цвета пройдут прямо, а петле нужно поворачиваться пред и / или после ячейки на своем пути;
2) Кружки черного цвета будут включены, но петле нужно пройти включая клетки (предыдущая, а также следующая) на своем пути.
Мосты строить разгадать бесплатно (Hashi, Hashiwokakero, Bridges, Chopsticks, Ai-Ki-Ai)
На crossword.nalench.com мы предлагаем вам сильное привыкание к этому типу головоломок хаши (или аши о kakero головоломки). Без какого-либо неуважения к прекрасному японскому языку, мы предпочитаем имя Мосты, так как название hashiwokakero, вероятно, труднее, чем загадка, чтобы решить.
У нас есть головоломки Мосты 3-х уровней: легкий 6 на 6, более сложный 9 на 9 и крекинг сетки размеров от 12 до 18. Нажмите здесь или на изображении выше, чтобы перейти на страницу загрузки головоломок.
Все наши головоломки в онлайн виде, виходят с ответами и легко распечатать. Они свободны, нет никаких раздражающих всплывающих окон и нет необходимости в регистрации. Чистые, простые и сделанные для поклонников японских головоломок.
Мосты (Bridges) отличные головоломки для досуга и образовательных целей, как они сочетают в себе удовольствие, логические и математические навыки.
Основные правила постройки мостов
Строить мосты фантастическая визуальная головоломка на логику, которая немедленно вас зацепит. В сетках разных размеров вы найдете острова и номера и должны соединить остров с помощью так называемых мостов. Эта логическая головоломка будет способна проверить ваш пространственный интеллект по максимуму.
1. Изобразите мосты (линии) между островами (пронумерованными кружками)

В онлайн головоломке Мосты (Hashiwokakero) сетки заполняются с пронумерованными кругами. Цель загадки состоит в том, чтобы соединить все острова (кружки), рисуя линии (мосты между ними). Все острова должны быть подключены.
2. Количество мостов, соединяющих остров должно равняться числу в круге

Правила Мостов (Hashiwokakero) каждый остров имеет номер, указанный в нем, и количество линий, мостов, которые соединяют и должны быть равны этому числу. В примере слева вы можете увидеть, что синий остров соединен 2 мостами и что остров с 4 в нем соединен с 4 одиночными мостами.
3. Максимальное количество мостов, соединяющих два острова 2

Максимальное количество линий между островами составляет 2, либо допускается один мост или двойной мост. Вам не разрешено рисовать, скажем, 3 моста между 3 и 4 в нашем примере слева.
4. Мосты соединяют острова по горизонтали или по вертикали

головоломки мосты, соединяющие острова рисуются по горизонтали или по вертикали. Вы не можете соединить острова по диагонали. Пример слева показывает неправильное решение, то 2 из них и 2 связаны с диагональными линиями! Такое невозможно!
5. Мосты не могут пересекаться друг с другом

Правила Строить мосты: Другое важное правило заключается в том, что мосты не могут пересекаться друг с другом. В этом примере мы видим, мост между 3 и 1 своего креста, который не допускается.
6. Мосты и острова должны образовывать единую связную группу
 Стратегии Hashiwokakero: Все острова соединены мостами, которые образуют единую, связанную группу, которая не пересекает себя (правило 5). В нашем примере мы имеем 2 группы островов. В 2 Двойки одна группа, которая не допускается.
Стратегии Hashiwokakero: Все острова соединены мостами, которые образуют единую, связанную группу, которая не пересекает себя (правило 5). В нашем примере мы имеем 2 группы островов. В 2 Двойки одна группа, которая не допускается.Как решать Хаши?
Следуя сообразно стопам судоку, Kakuro и остальных Количество закономерных головоломок, Хаши еще 1 семья просто выяснить привыкание закономерные головоломки, которые были открыты в Стране восходящего солнца. Внедрение незапятанной логики и никак не требующий арифметику, чтоб постановить данные интереснейшие головоломки дают нескончаемое наслаждение и интеллектуальное веселие, чтоб смущать почитателей всех умений и возрастов.
Хаши считается мостом-включения головоломки. В различие от остальных закономерных головоломок, Хаши находят решение маршрутом соединения острова с мостами в согласовании с правилами, этак будто все мосты объединены меж собой, дозволяющие проход от хоть какого острова к иному.
Хаши головоломки посещают различных объемов и варьируются от совсем просто совсем тяжело воспринимать будто-нибудь от 5 мин. по нескольких часов, чтоб постановить. Тем никак не наименее, изготовить 1 оплошность, и вы окажетесь завязнул позднее, как вы теснее к решению...
Ежели вы предпочитаете судоку, Kakuro и остальные закономерные головоломки, вы будете обожать кроссворды Хаши, как отлично!
Строгие Хаши
Любая головоломка базирована на прямоугольном месторасположении островков, в каком месте количество в любом полуострове указывает, насколько мостов объединены с ней. Мишень состоит в том, чтоб объединить все острова в согласовании с численностью мостов этак:
Имеется никак не наиболее 2-ух мостов в том ведь направленности.
Мосты имеют все шансы существовать лишь вертикальными либо горизонтальными и никак не имеют права переходить острова либо остальные мосты.
Опосля окончания возведения, все мосты объединены меж собой дозволяет проход от хоть какого острова к иному.
Рассмотрим головоломку Мосты (9x9 Легкий)
Hashi-o-kakero (Мосты) это логическая головоломка. Цель состоит в том, чтобы соединить все острова в одну связную группу.
Как играть в Мосты (Хаши)?
Цель игры состоит в том, чтобы соединить острова, проведя ряд мостов между островами. Число в центре каждого острова представляет собой количество мостов, подключенных к нему. Мосты должны начинаться и заканчиваться на отдельных островах, путешествуя по прямой линии между ними и не пересекая любые другие мосты или острова. Только один или два моста могут подключить пару островов. Для того, чтобы построить мост между двумя островами нажмите на первый (он будет отображаться как выбран), затем нажмите на другой. Если вы хотите еще один мост между этими двумя острова повторите процедуру. Если вы сделаете это снова эти два моста исчезнут.
Пример решения кроссворда Мосты:
В начале игры будут только островы и никаких мостов, соединяющих их и будет выглядеть что-то похожее на это изображение:

Чтобы решить загадку, Вы должны соединить все острова, принимая во внимание количество в каждом острове - это представляет точное число мостов, чтобы достигнуть его. Два соседние острова могут или не могут быть соединены вместе с одним или двумя мостами. Мосты не могут пересекаться друг с другом. Они могут быть размещены только по горизонтали или по вертикали на таблице. Кроме того, важно знать, что каждая пара островов должна быть соединена либо непосредственно, либо быть в каком-то «косвенном» соединении.
Вот один из способов, чтобы решить головоломку, приведенную выше. «Самый простой» здесь это остров, который находится в левом нижнем углу таблицы. Он может быть связан только с соседним островом справа и может иметь только один мост. Для того, чтобы присоединиться к ним мы нажимаем на нее:

После этого мы нажимаем на острове справа и появляется мост:

Мы по-прежнему таким же образом можем построить больше мостов, которые очевидны:

На следующем рисунке показано, как мы подключили верхние острова:

Это совершенно неправильно, так как эта группа мостов будет «изолирована» от других. Но правило говорит, что между любыми 2 островами должны иметь прямое или косвенное соединение. Таким образом, мы должны удалить эти мосты. Это может быть сделано еще один виртуальный остров между островами
И вот как это должно быть:

На острове в середине должен иметь 5 мостов, но мы построили только 2. Так как уже есть 2 моста, и мы не можем построить еще один единственный выбор, чтобы построить эти 3 оставшиеся мосты между 2 горизонтально соседними островами. Таким образом, мы должны иметь по крайней мере один мост слева и справа.

Вслед за этим приходят подобные мысли:

Есть 2 Остальные опции - либо соединить остров «5» с островом «4», а затем головоломка становится тривиальной:

или соединить два соседних вертикальных острова с двумя мостами и, следовательно, прийти к другому решению:
Не каждая головоломка может иметь несколько решений. Мы выбираем именно это, чтобы показать вам более широкий диапазон возможных игр Мосты.
ПОЛЕЗНЫЕ ссылки
Более подробную информацию можно найти на сайте Википедии: (головоломка Bridges).
Мосты (Хаши) чисельные кроссворды разгадывают на таблице с ячейками, часть которых имеют кружки; Любой кружок либо «белого цвета» (пустая ячейка), либо «черного цвета» (заполненная ячейка). Цель состоит в том, чтобы нарисовать одну непрерывную непересекающуюся петлю, которая правильным образом должна пройти сквозь окруженные квадратики. Петля «вводит» каждую клетку, которую она пересекает, по центру одной из своих четырех сторон и «выходить» с другой стороны; Поэтому любые изгибы составляют 90 градусов.
У двух разновидностей кружков есть разные требования к тому, как циклу нужно пройти их пересекая:
1) Кружки белого цвета пройдут прямо, а петле нужно поворачиваться пред и / или после ячейки на своем пути;
2) Кружки черного цвета будут включены, но петле нужно пройти включая клетки (предыдущая, а также следующая) на своем пути.
Петро Полюхович © 2011-2024
Join us if you are a true crossword puzzler!


 Login
Login Crosswords
Crosswords Conundrums
Conundrums Sudoku
Sudoku English
English Turkish
Turkish About
About