Войти
Кроссворды
Головоломки
Судоку
Скачать/распечатать
Английские
Турецкие
О сайте
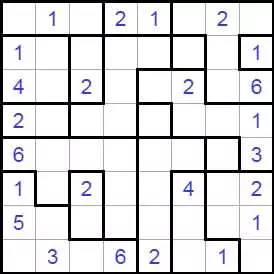
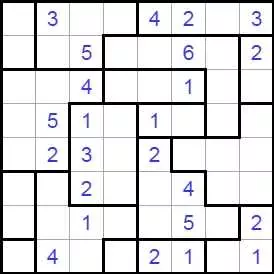
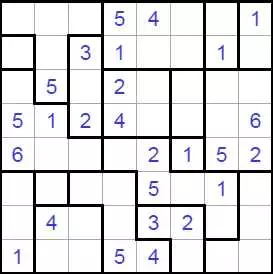
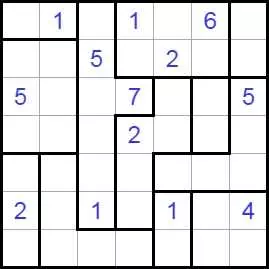
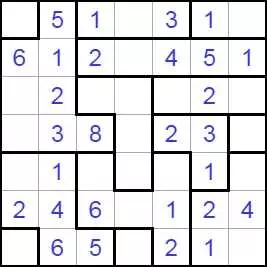
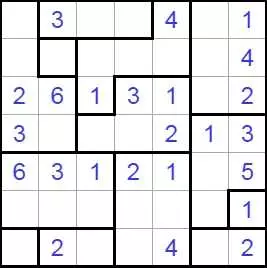
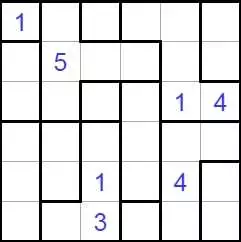
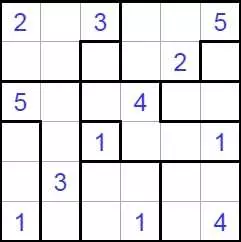
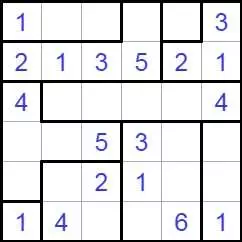
Волновой эффект разгадать
В Волновой эффект (Ripple Effecti, Hakyuu) играют на прямоугольной сетке, разделенной на блоки (полиномино). Решатель должен поместить одно положительное целое в каждую ячейку сетки - некоторые из которых могут быть заданы заранее - согласно этим правилам:
Каждый полиомино должен содержать последовательные целые числа от 1 до количества клеток в этом полиомино включительно.
Если в одной и той же строке или столбце появляются два одинаковых числа, по крайней мере, многие ячейки с другими номерами должны их отделять. Например, две ячейки, содержащие «1», могут быть не ортогонально смежными, но должны иметь по меньшей мере одну ячейку между ними с другим номером. Две ячейки, помеченные «3» в одной строке или столбце, должны иметь по крайней мере три ячейки с другими номерами между ними в этой строке или столбце и так далее.
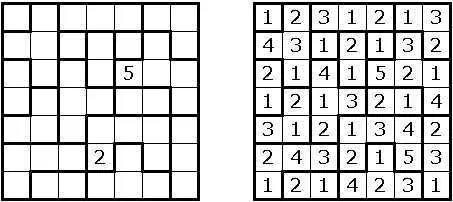
Заполните ячейки области цифрами от 1 до n (размер) области. Если есть две ячейки с одинаковым числом n в строке или столбце, между этими двумя ячейками должно быть не менее n ячеек. Вот небольшой пояснительный пример: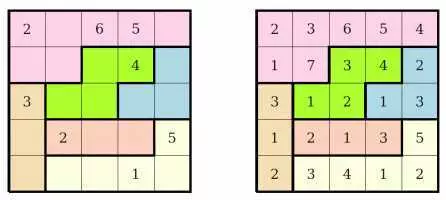
Головоломка Волновой эффект также известна как Ripple Effecti или Hakyuu Kouka.
1. Впишите единственное позитивное единое количество в любую порожнюю клетку.
2. Каждая область сетки обязана иметь поочередные цифры, начинающиеся с 1, вверх по количеству ячеек в этом регионе. (Например, 4-элементная область должна содержать номера от 1 до 4)
3. Любые два вхождения одного и того же числа в одной строке или столбце должны иметь по крайней мере такое количество других ячеек между ними. (Например, два 2 в одной строке или столбце должны иметь по крайней мере две другие ячейки между ними.)
Я думаю, что правило 3 неоднозначно: «между двумя вхождениями» заставляет звучать так, как будто два - максимальное количество разрешений. Тем не менее, я вижу из решения, что допускается более двух вхождений в строку.
Правила Волновой эффект
В Волновой эффект (Ripple Effecti, Hakyuu) играют на прямоугольной сетке, разделенной на блоки (полиномино). Решатель должен поместить одно положительное целое в каждую ячейку сетки - некоторые из которых могут быть заданы заранее - согласно этим правилам:
Каждый полиомино должен содержать последовательные целые числа от 1 до количества клеток в этом полиомино включительно.
Если в одной и той же строке или столбце появляются два одинаковых числа, по крайней мере, многие ячейки с другими номерами должны их отделять. Например, две ячейки, содержащие «1», могут быть не ортогонально смежными, но должны иметь по меньшей мере одну ячейку между ними с другим номером. Две ячейки, помеченные «3» в одной строке или столбце, должны иметь по крайней мере три ячейки с другими номерами между ними в этой строке или столбце и так далее.
Головоломка Хакюу
Заполните ячейки области цифрами от 1 до n (размер) области. Если есть две ячейки с одинаковым числом n в строке или столбце, между этими двумя ячейками должно быть не менее n ячеек. Вот небольшой пояснительный пример:
Головоломка Волновой эффект также известна как Ripple Effecti или Hakyuu Kouka.
1. Впишите единственное позитивное единое количество в любую порожнюю клетку.
2. Каждая область сетки обязана иметь поочередные цифры, начинающиеся с 1, вверх по количеству ячеек в этом регионе. (Например, 4-элементная область должна содержать номера от 1 до 4)
3. Любые два вхождения одного и того же числа в одной строке или столбце должны иметь по крайней мере такое количество других ячеек между ними. (Например, два 2 в одной строке или столбце должны иметь по крайней мере две другие ячейки между ними.)
Я думаю, что правило 3 неоднозначно: «между двумя вхождениями» заставляет звучать так, как будто два - максимальное количество разрешений. Тем не менее, я вижу из решения, что допускается более двух вхождений в строку.
Петро Полюхович © 2011-2024
Присоединяйтесь к нам, если вы настоящий ценитель кроссвордов!