Следующая Эйлеров квадрат 3х3 #3 Легкий
 Эйлеров квадрат 3х3 #1 Легкий Предыдущая
Эйлеров квадрат 3х3 #1 Легкий Предыдущая
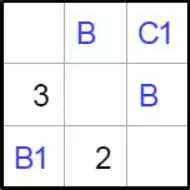
Эйлеров квадрат #2 Легкий (Греко-латинский квадрат, Квадрат Эйлера, Eulero) - Размер: 3х3

 Эйлеров квадрат 3х3 #1 Легкий Предыдущая
Эйлеров квадрат 3х3 #1 Легкий ПредыдущаяЭйлеров квадрат #2 Легкий (Греко-латинский квадрат, Квадрат Эйлера, Eulero) - Размер: 3х3
|
|
|
|
Пазлы Эйлера, мы все видели эти геометрические головоломки, которые бросают вызов вам проследить вдоль всех линий, не отрывая ручку от бумаги и отслеживая каждую линию только один раз. Сколько из этих головоломок вы можете закончить? Сколько из этих головоломок возможно и сколько невозможно? Есть ли способ узнать, возможна ли такая головоломка, не пытаясь ее попробовать? Там есть. Сначала попробуйте их, а затем проверьте ответы, а также изучите секрет.
Когда вы знакомы с Правилами Квадрата Эйлера, легко разгадать онлайн загадки, подобные этой Эйлеров квадрат 3х3 #2 Легкий, и быть уверенным в том, возможны ли они или нет - все, что вам нужно, - это перо: отлично подходит для перерывов на кофе, и т.п.
Когда вы знакомы с Правилами Квадрата Эйлера, легко разгадать онлайн загадки, подобные этой Эйлеров квадрат 3х3 #2 Легкий, и быть уверенным в том, возможны ли они или нет - все, что вам нужно, - это перо: отлично подходит для перерывов на кофе, и т.п.

Ответ на Эйлеров квадрат 3х3 #2 Легкий
Комментарии:
Будьте первыми, кто прокомментирует кроссворд!
Новые комментарии кроссвордистов:
Петро Полюхович © 2011-2024
Присоединяйтесь к нам, если вы настоящий ценитель кроссвордов!


 Войти
Войти Кроссворды
Кроссворды Головоломки
Головоломки Судоку
Судоку Английские
Английские Турецкие
Турецкие О сайте
О сайте