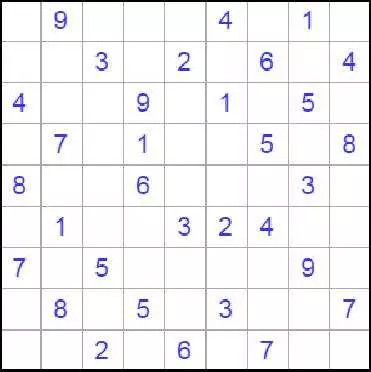
Логические головоломки 2D Судоку
Эти числовые кроссворды также известны как: Латинский квадрат, Latin Square
2D Sudoku превращает судоку в следующее измерение, по крайней мере, с точки зрения его внешнего вида. Головоломка решается, как обычный судоку, без множества перекрывающихся сеток и областей, за исключением того, что в 2D-судоку эти ограничения более разнообразны и состоят из перекрывающих друг друга рядов в одном из двух разных направлений.
В частности, в этом разделе мы предлагаем 2D Судоку, разных уровней сложности: легкий, средний, трудный и очень трудный, чтобы решить - вы не найдете более интересного и более впечатляющего варианта судоку! Цель остается простой: просто поместите числа от 1 до 9 в каждую пустую ячейку, чтобы оно не повторялось в горизонтальном ряду и вертикальной колонке. Толстые черные линии указывают границы, где строки не продолжаются, поэтому с точки зрения логической сложности это точно так же, как и обычном судоку. В плане решения, однако, он чувствует себя совсем по-другому, и обычно головоломки включают в себя «погоню» вокруг сетки, которая тщательно спроектирована так, что ничего не соединяется через середину, и поэтому числа движутся в обоих направлениях вокруг внешней стороны головоломки.
Как и во всех наших логических головоломках, существует только одно возможное решение. Более того, мы гарантируем, что всегда можно достичь разумной логической дедукции, поэтому угадывание никогда не требуется.
И так, посетители нашего сайта, мы подумали, что вас может заинтересовать следующий метод решения головоломок типа 2D SUDOKU.
Чтобы было легче понять, мы применили наш алгоритм к маленькой головоломке 4х4, но вы можете применить ту же технику к более крупным головоломкам, например, 9х9.
ПРАВИЛА 2D Судоку: Символы 1, 2, 3, 4 должны быть введены в пустые ячейки квадрата 4x4, показанные ниже, таким образом, чтобы каждое число встречалось один раз в каждой строке, один раз в каждом столбце и один раз в каждом цветном 2x2 подквадрате.
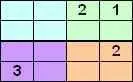 Один хороший способ найти решение этой головоломки - это взять каждую пустую ячейку и написать список возможных символов, которые можно поместить в эту пустую ячейку. Мы строим эти списки с использованием фактов, что каждый символ может встречаться один раз в каждой строке, один раз в каждом столбце и один раз в каждом подквадрате 2x2.
Один хороший способ найти решение этой головоломки - это взять каждую пустую ячейку и написать список возможных символов, которые можно поместить в эту пустую ячейку. Мы строим эти списки с использованием фактов, что каждый символ может встречаться один раз в каждой строке, один раз в каждом столбце и один раз в каждом подквадрате 2x2.
В этом примере список возможных символов для пустых ячеек показан в массиве справа. Темные квадраты показывают, что эти ячейки уже заполнены.
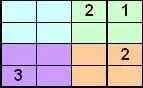
Мы сразу видим, что две пустые ячейки углов должны содержать символ 4. И мы обновляем наш квадрат, а затем обновляем наши списки для оставшихся пустых ячеек.
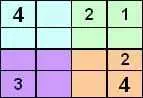
Теперь мы можем видеть, что еще два «1» вытеснены, а значит, еще два «3». Итак, мы обновляем нашу площадь и, если захотим, мы сможем легко закончить площадь в этот момент. Но ради выполнения нашего алгоритма мы обновим наши списки и продолжим процесс.
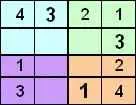
Ведущий к:
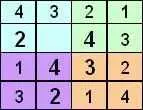

И поэтому наше решение будет выглядеть так:
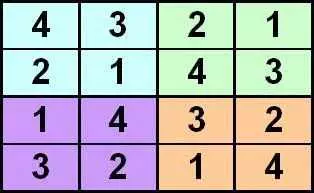
НОВЫЕ ПРАВИЛА 2D Судоку: символы 1, 2, 3, 4 должны быть введены в пустые ячейки квадрата 44, показанные ниже, таким образом, что каждый символ встречается один раз в каждой строке, один раз в каждом столбце, один раз в каждом Квадратный зеленый цвет, один раз в каждом квадрате, окрашенный в синий цвет, один раз в каждый квадрат, окрашенный в оранжевый цвет и один раз в каждый квадрат, окрашенный в фиолетовый цвет.
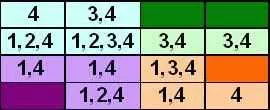
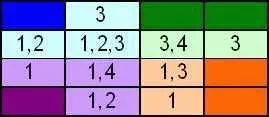
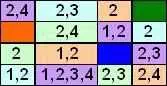
 Для этого квадрата список возможных символов (не забудьте использовать ваши правила), которые могут быть помещены в каждую пустую ячейку:
Для этого квадрата список возможных символов (не забудьте использовать ваши правила), которые могут быть помещены в каждую пустую ячейку:
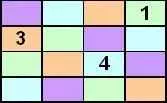
 Сразу видно, что три 2, которые вынуждены в ячейках в строках 1, 2 и 3, и мы можем обновить наш квадрат следующим образом.
Сразу видно, что три 2, которые вынуждены в ячейках в строках 1, 2 и 3, и мы можем обновить наш квадрат следующим образом.
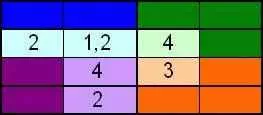
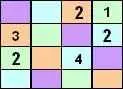 Наконец, обновляя список возможных символов, который теперь может быть помещен в пустые ячейки, дает:
Наконец, обновляя список возможных символов, который теперь может быть помещен в пустые ячейки, дает:
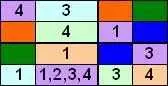
Теперь очевидно, что наше решение должно быть:
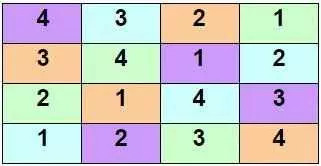
Последний квадрат, показанный выше, является примером ортогонального латинского квадрата.
Сейчас мы определим ортогональный латинский квадрат как массив nxn, где ячейки будут окрашены с использованием n цветов таким образом, чтобы каждый цвет происходил один раз в каждой строке и один раз в каждом столбце, и мы помещаем символы 1 в n в Так что каждый символ встречается один раз в каждой строке, один раз в каждом столбце, а для каждого цвета и каждого символа есть ровно одна ячейка, затененная этим цветом и содержащая этот символ.
Если вы проверите квадрат 4x4, вы увидите, что он удовлетворяет этому определению для n=4.
Теперь сделаем еще сложнее. Посмотрите на следующий квадрат

Он удовлетворяет определению ортогонального латинского квадрата, но у него есть добавленное свойство, если мы посмотрим на шаблоны в ячейках, то каждый шаблон встречается один раз в каждой строке, один раз в каждом столбце. Далее для каждого шаблона и каждого символа имеется ровно одна ячейка, которая содержит эту комбинацию, и для каждого шаблона и каждого цвета есть ровно одна ячейка, которая содержит эту комбинацию.
Математически мы думаем о разделении этого массива на три массива, как показано на примере:

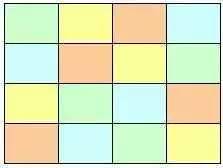

Вместе мы говорим, что эти три квадрата образуют набор из трех взаимно ортогональных латинских квадратов.
Математически можно доказать, что для массивов размером 5х5, 7х7, 8х8, 9х9 и NхN, где N больше 10, мы всегда можем найти три массива, обладающих указанными выше свойствами. Также известно, что 3 таких массива 6х6 невозможно найти.
Но никто не знает, можем ли мы найти три таких массива с размером сетки 10х10? Это открытый вопрос, который изучают многие исследователи. Если вы хотите узнать больше об этой важной проблеме, почитайте в инете.
2D Sudoku превращает судоку в следующее измерение, по крайней мере, с точки зрения его внешнего вида. Головоломка решается, как обычный судоку, без множества перекрывающихся сеток и областей, за исключением того, что в 2D-судоку эти ограничения более разнообразны и состоят из перекрывающих друг друга рядов в одном из двух разных направлений.
В частности, в этом разделе мы предлагаем 2D Судоку, разных уровней сложности: легкий, средний, трудный и очень трудный, чтобы решить - вы не найдете более интересного и более впечатляющего варианта судоку! Цель остается простой: просто поместите числа от 1 до 9 в каждую пустую ячейку, чтобы оно не повторялось в горизонтальном ряду и вертикальной колонке. Толстые черные линии указывают границы, где строки не продолжаются, поэтому с точки зрения логической сложности это точно так же, как и обычном судоку. В плане решения, однако, он чувствует себя совсем по-другому, и обычно головоломки включают в себя «погоню» вокруг сетки, которая тщательно спроектирована так, что ничего не соединяется через середину, и поэтому числа движутся в обоих направлениях вокруг внешней стороны головоломки.
Как и во всех наших логических головоломках, существует только одно возможное решение. Более того, мы гарантируем, что всегда можно достичь разумной логической дедукции, поэтому угадывание никогда не требуется.
И так, посетители нашего сайта, мы подумали, что вас может заинтересовать следующий метод решения головоломок типа 2D SUDOKU.
Чтобы было легче понять, мы применили наш алгоритм к маленькой головоломке 4х4, но вы можете применить ту же технику к более крупным головоломкам, например, 9х9.
Сначала изложим суть головоломки
ПРАВИЛА 2D Судоку: Символы 1, 2, 3, 4 должны быть введены в пустые ячейки квадрата 4x4, показанные ниже, таким образом, чтобы каждое число встречалось один раз в каждой строке, один раз в каждом столбце и один раз в каждом цветном 2x2 подквадрате.

В этом примере список возможных символов для пустых ячеек показан в массиве справа. Темные квадраты показывают, что эти ячейки уже заполнены.


Мы сразу видим, что две пустые ячейки углов должны содержать символ 4. И мы обновляем наш квадрат, а затем обновляем наши списки для оставшихся пустых ячеек.


Теперь мы можем видеть, что еще два «1» вытеснены, а значит, еще два «3». Итак, мы обновляем нашу площадь и, если захотим, мы сможем легко закончить площадь в этот момент. Но ради выполнения нашего алгоритма мы обновим наши списки и продолжим процесс.


Ведущий к:


И поэтому наше решение будет выглядеть так:

Что, если мы изменим правила головоломки?
НОВЫЕ ПРАВИЛА 2D Судоку: символы 1, 2, 3, 4 должны быть введены в пустые ячейки квадрата 44, показанные ниже, таким образом, что каждый символ встречается один раз в каждой строке, один раз в каждом столбце, один раз в каждом Квадратный зеленый цвет, один раз в каждом квадрате, окрашенный в синий цвет, один раз в каждый квадрат, окрашенный в оранжевый цвет и один раз в каждый квадрат, окрашенный в фиолетовый цвет.




Теперь очевидно, что наше решение должно быть:

Последний квадрат, показанный выше, является примером ортогонального латинского квадрата.
Сейчас мы определим ортогональный латинский квадрат как массив nxn, где ячейки будут окрашены с использованием n цветов таким образом, чтобы каждый цвет происходил один раз в каждой строке и один раз в каждом столбце, и мы помещаем символы 1 в n в Так что каждый символ встречается один раз в каждой строке, один раз в каждом столбце, а для каждого цвета и каждого символа есть ровно одна ячейка, затененная этим цветом и содержащая этот символ.
Если вы проверите квадрат 4x4, вы увидите, что он удовлетворяет этому определению для n=4.
Теперь сделаем еще сложнее. Посмотрите на следующий квадрат

Он удовлетворяет определению ортогонального латинского квадрата, но у него есть добавленное свойство, если мы посмотрим на шаблоны в ячейках, то каждый шаблон встречается один раз в каждой строке, один раз в каждом столбце. Далее для каждого шаблона и каждого символа имеется ровно одна ячейка, которая содержит эту комбинацию, и для каждого шаблона и каждого цвета есть ровно одна ячейка, которая содержит эту комбинацию.
Математически мы думаем о разделении этого массива на три массива, как показано на примере:



Вместе мы говорим, что эти три квадрата образуют набор из трех взаимно ортогональных латинских квадратов.
Математически можно доказать, что для массивов размером 5х5, 7х7, 8х8, 9х9 и NхN, где N больше 10, мы всегда можем найти три массива, обладающих указанными выше свойствами. Также известно, что 3 таких массива 6х6 невозможно найти.
Но никто не знает, можем ли мы найти три таких массива с размером сетки 10х10? Это открытый вопрос, который изучают многие исследователи. Если вы хотите узнать больше об этой важной проблеме, почитайте в инете.
Петро Полюхович © 2011-2024
Join us if you are a true crossword puzzler!


 Login
Login Crosswords
Crosswords Conundrums
Conundrums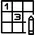 Sudoku
Sudoku English
English Turkish
Turkish About
About