Правила и стратегии решения Сумдоку Killer sudoku

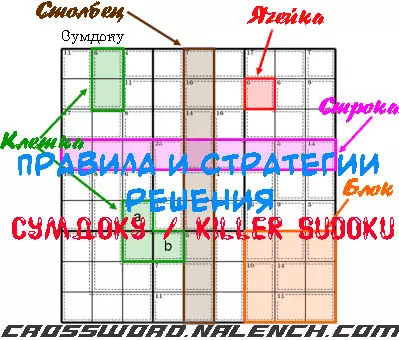
Статья про Правила и стратегии решения Сумдоку Killer sudoku

Содержание

• Правила Сумдоку
  
• Резюме
  
• Терминология
  
• Правила
  
• Правила для Сумдоку Больше-Меньше
  
• Правила для Судоку Больше-Меньше
  
• Введение
  
• Базовые стратегии решения
  
• Пример базовой головоломки
  
• Более сложный пример, основанный на Сумдоку №24
  
• Более сложный пример, основанный на Сумдоку №28
  
• Более сложный пример, основанный на Сумдоку №74
  
• Сумдоку (№1271) проще, чем кажется
  
• Более сложный пример, основанный на Сумдоку №183
  

Правила сумдоку / Killer Sudoku

Резюме

Правила Сумдоку или Killer Sudoku просты. Применяются правила как для обычных судоку с одним дополнительным правилом: сумма клеток в блоке выделенном пунктирной линией должна равняться сумме, указанной вверху этого блока. Каждая цифра в клетке должна быть уникальной.

Терминология

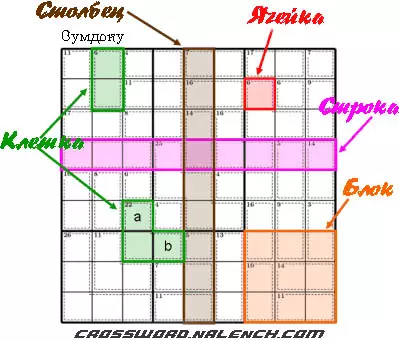
Ячейка - Единая коробка. Он может содержать любую цифру от одного до девяти.
Ряд - Горизонтальная группа из девяти ячеек. Каждая ячейка в строке должна содержать разные цифры.
Столбец - Вертикальная группа из девяти ячеек. Каждая ячейка в столбце должна содержать разные цифры.
Блок - Сетка ячеек 3x3. Он обведен жирными линиями. Каждая ячейка в nonent должна содержать разные цифры.
Клетка - Группа ячеек, обведенная пунктирной линией. Сумма значений ячеек в клетке должна равняться сумме, указанной в правом верхнем углу клетки.
Значения в клетке должны быть уникальными, даже если правила обычного сумдоку допускают дублирование. Например, ячейки с метками «a» и «b» на рисунке не могут иметь одинаковое значение.
Область - Область головоломки, которая не может содержать повторяющиеся цифры. То есть строка, столбец, блок или клетка.

Правила

Как и в обычных сумдоку, каждая ячейка в каждой строке, столбце и блоке должна содержать уникальную цифру. Другими словами, каждая строка, столбец и блок должны содержать все цифры от одного до девяти.

Сумма значений ячеек в клетке должна равняться сумме для этой клетки.

Значения ячеек в клетке должны быть уникальными.

Правила для Сумдоку Больше-Меньше

Применяются правила Killer Sudoku. Если между клетками есть '>', '<' или, '=', тогда сумма значений в клетках должна подчиняться указанным отношениям.

Правила для Судоку Больше-Меньше

Действуют правила обычного сумдоку. Значения каждой ячейки должны подчиняться отношениям между ячейками, указанными с помощью '>' или '<'.

Стратегии решения Сумдоку / Killer Sudoku

Есть три основных метода, используемых для решения головоломок сумдоку.
Первый - использовать стратегии для решения обычных головоломок сумдоку.
Во-вторых, необходимо рассмотреть различные способы создания суммы.
В-третьих, нужно учитывать общую стоимость региона. Здесь мы обрисовываем основные стратегии, а затем показываем, как они применяются в примере головоломки. Позже мы опубликуем более сложные стратегии.
(Терминология, используемая на этой странице, определяется на странице правил)

Основные стратегии решения

Ниже приведены основные правила, используемые для решения Убийцы Судоку.

Правило 1

Это напрямую связано с определением сумдоку. Ни один регион не может содержать повторяющиеся цифры. В области сумдоку каждая цифра появляется ровно один раз . Например, если цифра появляется в строке, ее не может быть ни в одной другой ячейке в строке. Точно так же каждая цифра может появиться в клетке только один раз. Если цифра находится в клетке, она не может снова появиться в этой клетке.

Правило необходимости

Это правило может применяться к областям сумдоку (например, ряду, столбцу или блоку) или к клетке. В первом случае каждый регион должен содержать все цифры от одной до девяти. Таким образом, если все цифры, кроме одной, появляются в строке, отсутствующая цифра должна появиться в пустой ячейке.

Правило 45

Каждая область сумдоку (то есть строка, столбец или блок) содержит цифры от первой до девятой. Таким образом, каждая область сумдоку имеет общее значение 45. Если S - это сумма всех клеток, полностью содержащихся в области, тогда сумма непокрытых клеток должна составлять 45-S.

Правило К

Правило k является расширением правила 1. Если есть k ячеек, полностью содержащихся в области, которая содержит ровно k различных возможных значений, то никакая другая ячейка в этой области не может содержать любое из этих k значений.

Сумма исключения

Эта стратегия исследует различные возможные способы получения суммы клетки. Уменьшение количества различных возможных способов получения суммы часто может привести к потенциальному решению. Есть много способов уменьшить количество сумм. Например, если в 2 клетке всего 3, 4, 16 или 17, то можно использовать только одну комбинацию значений. (3 = 2 + 1, 4 = 3 + 1, 16 = 9 + 7 и 17 = 9 + 8.) 3 клетки с одной комбинацией: 6 = 1 + 2 + 3, 7 = 1 + 2 + 4, 23 = 9 + 8 + 6, 24 = 9 + 8 + 7. Калькулятор сумм на странице онлайн-плеера может оказаться очень полезным.

еще не все...

Применение основных стратегий. Пример

Здесь мы будем использовать описанные выше стратегии для решения головоломки Killer Sudoku. Возможно, вы захотите распечатать сетку сумдоку, чтобы выполнять все шаги.

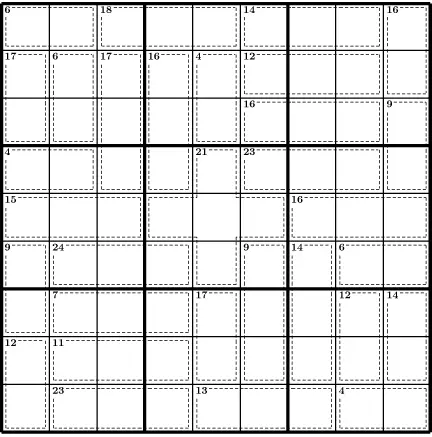
Правило 45

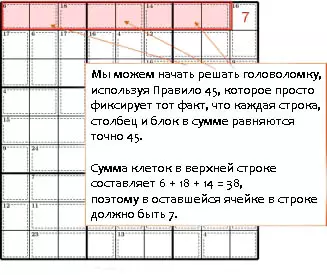
Правило необходимости

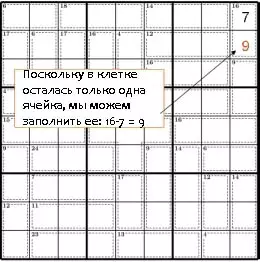
Правило 1

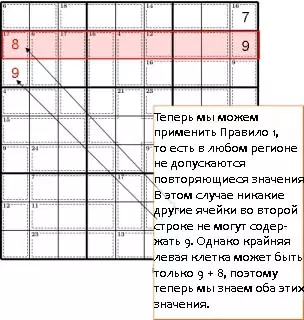
Уникальные суммы

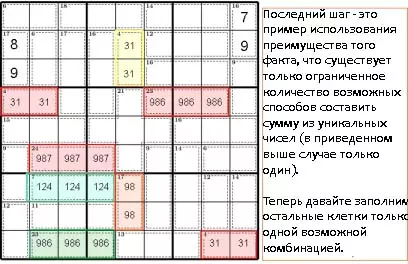
Правило К

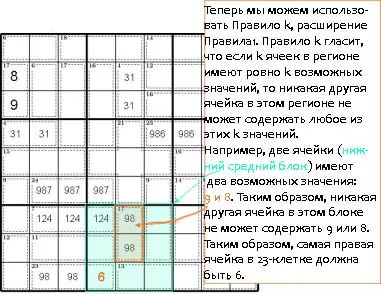
Правило K
Ограниченные возможные суммы

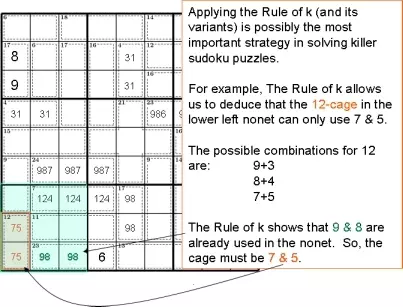
Применение Правила k (и его вариантов), возможно, является наиболее важной стратегией в решении головоломок сумдоку.
Например. Правило k позволяет нам сделать вывод, что 12-клетка в нижнем левом нонете может использовать только 7 и 5.
Возможные комбинации для 12:
9 + 3
8 + 4
7 + 5
Правило k показывает, что 9 и 8 уже используются в нонете. Итак, клетка должна быть 7 и 5.

Правило необходимости

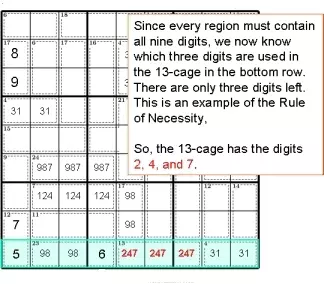
Поскольку каждый регион должен содержать все девять цифр, теперь мы знаем, какие три цифры используются в клетке 13 в нижнем ряду. Осталось всего три цифры. Это пример правила необходимости:
Итак, в 13-клетке есть цифры
2, 4 и 7.

Ограниченные возможные суммы

Ранее мы заполняли клетки, в сумме которых была только одна возможная комбинация.
Теперь у нас достаточно информации, чтобы посмотреть на другие клетки, в которых было более одной возможной комбинации. Например, единственный способ получить 9 в клетке из двух ячеек:
8 + 1
7 + 2
6 + 3
5 + 4
Но в крайнем левом столбце уже 5,7,8 и 9.
Таким образом, 9-клетка должна быть 6 и 3.

Правило К

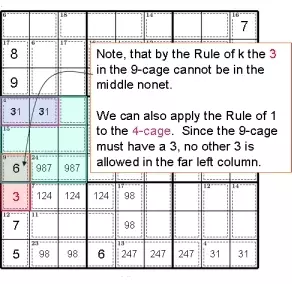
Обратите внимание, что по правилу k тройка в клетке из 9 не может находиться в среднем ноне.
Мы также можем применить Правило 1 к 4-клетке. Поскольку в клетке с 9 цифрами должна быть 3, никакие другие 3 в крайнем левом столбце не допускаются.

Правило ограниченных возможных сумм 1
Правило К

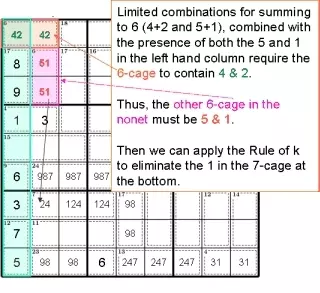
Ограниченные комбинации для суммирования до 6 (4 + 2 и 5 + 1) в сочетании с наличием 5 и 1 в левом столбце требуют, чтобы клетка из 6 содержала 4 и 2.
Таким образом, остальные 6 клеток в блоке должны быть 5 и 1.
Затем мы можем применить Правило k, чтобы исключить 1 в клетке из 7 внизу.

Правило необходимости
Правило 1
всех возможных сумм

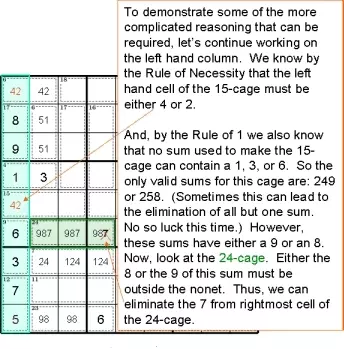
Чтобы продемонстрировать некоторые из более сложных рассуждений, которые могут потребоваться, давайте продолжим работу с левым столбцом. Мы знаем по Правилу необходимости, что левая ячейка 16-клетки должна быть либо 4, либо 2.
И, согласно правилу 1, мы также знаем, что никакая сумма, используемая для создания 15-клетки, не может содержать 1, 3 или 6. Таким образом, единственные действительные суммы для этой клетки: 249 или 258. (Иногда это может привести к исключение всех сумм, кроме одной.
На этот раз не повезло.) Однако в этих суммах либо 9, либо 8. Теперь посмотрите на клетку с 24 клетками. Либо 8, либо 9 этой суммы должны быть вне блока. Таким образом, мы можем исключить 7 из крайней правой ячейки 24-клетки.

Правило необходимости:
ограниченные возможные суммы

Продолжая работать с левой частью, мы можем вывести значения для. Мы знаем, что оставшиеся цифры в верхнем левом блоке равны 3,6. и 7. По правилу 1, 7 не может быть в верхнем ряду. Так. 17-клетка должна содержать 7. Она также не может содержать 1 (поскольку 1 уже есть в обоих блоках). Кроме того, мы должны использовать одно из оставшихся чисел, оставшихся в верхнем левом блоке. Так. 17-клетка должна быть либо 76? или 73 ?. Если мы посмотрим на возможные суммы, осталось всего 467. Итак, теперь мы можем заполнить 4 ячейки! Оставшееся число в верхнем блоке - 3.
Верхняя часть блока 17-клетки - это 7 и 6. Средняя часть блока 17-клетки - 4.

Правило K
Правило 1  ограниченной возможной суммы

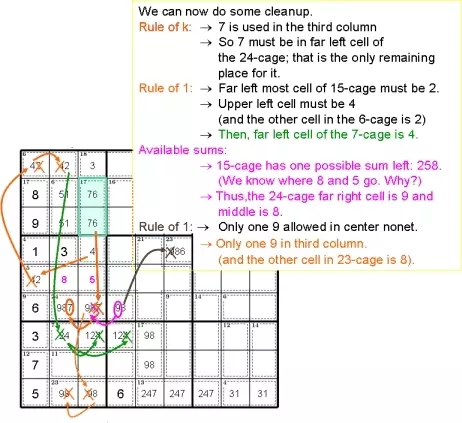
Теперь мы можем сделать некоторую очистку.

Правило k:
-> 7 используется в третьем столбце
-> Итак, 7 должна быть в крайней левой ячейке

24-клетка; это единственное оставшееся место для него.

Правило 1: Крайняя левая ячейка 15-клетки должна быть 2.
-> Верхняя левая ячейка должна быть 4
(а другая ячейка в 6-клетке - 2)
-> Тогда крайняя левая ячейка 7-клетки равна 4
-> У 15-клетки осталась одна возможная сумма: 258. (Мы знаем, куда идут 8 и 5. Почему?)
-> Таким образом, крайняя правая ячейка с 24 клетками - это 9, а средняя - 8.
Правило 1:
-> Только одна 9 разрешена в центре блока.
-> Только одна 9 в третьем столбце.
(а другая ячейка в 23 клетке - 8).

Оставшаяся сумма
Правило 1
Правило K
Правило необходимости

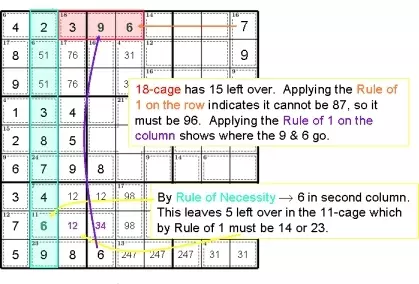
18 клеток осталось 15. Применение правила 1 в строке указывает, что не может быть 87, поэтому должно быть 96. Применение правила 1 в столбце показывает, куда идут 9 и 6.
По правилу необходимости -> 6 во втором столбце.
Таким образом, в клетке из 11 остается 5, которые по правилу 1 должны быть 14 или 23.

Сумма исключения

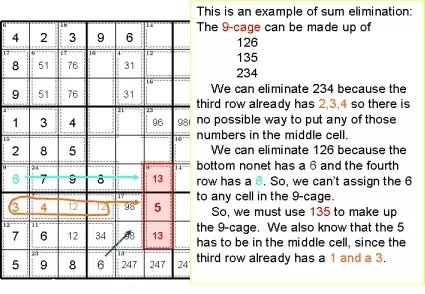
Это пример исключения суммы: 9-клетка может состоять из 126 135 234
Мы можем исключить 234, потому что в третьей строке уже есть 2, 3, 4, поэтому нет возможности поместить любое из этих чисел в среднюю ячейку.
Мы можем исключить 126, потому что у нижнего блока 6, а в четвертой строке 6. Итак, мы не можем присвоить 6 какой-либо ячейке в клетке из 9.
Итак, мы должны использовать 135, чтобы составить 9 клеток. Мы также знаем, что 5 должна быть в средней ячейке, поскольку в третьей строке уже есть 1 и 3.

Правило исключения суммы 1

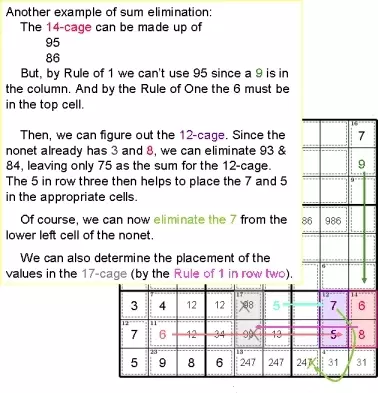
Другой пример исключения суммы:
14-клетка может состоять из 95 86
Но по правилу 1 мы не можем использовать 95, так как в столбце стоит 9. И по правилу одного шестерка должна быть в верхней ячейке.
Тогда мы сможем определить 12-клетку. Поскольку в блоке уже есть 3 и 8, мы можем исключить 93 и 84, оставив только 75 в качестве суммы для 12-клетки.
Затем 5 в третьем ряду помогает разместить 7 и 5 в соответствующих ячейках.
Конечно, теперь мы можем удалить 7 из нижней левой ячейки блока.
Мы также можем определить размещение значений в клетке из 17 (по правилу 1 во второй строке).

Диапазон
исключения итоговой суммы

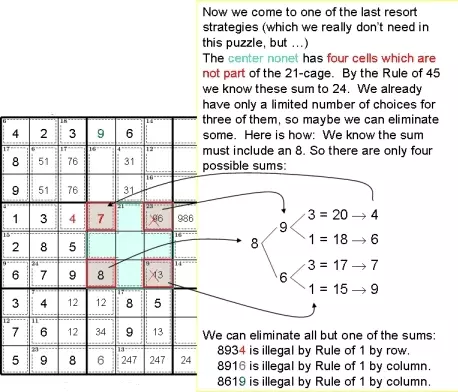
Теперь мы подошли к одной из последних стратегий (которая нам не нужна в этой головоломке, но ...)
В: enter no четыре ячейки, которые не являются частью 21 клетки. Согласно правилу 45 мы знаем, что их сумма равна 24. У нас уже есть ограниченное количество вариантов для трех из них, так что, возможно, мы сможем исключить некоторые из них. Вот как: мы знаем, что сумма должна включать 8. Итак, есть только четыре возможных суммы:
Мы можем исключить все суммы, кроме одной:
8934 является незаконным в соответствии с Правилом 1 к ряду.
8916 является незаконным согласно Правилу 1 по столбцу.
8619 является незаконным в соответствии с Правилом 1 по столбцу.

Правило 1
Правило необходимости
Оставшаяся сумма

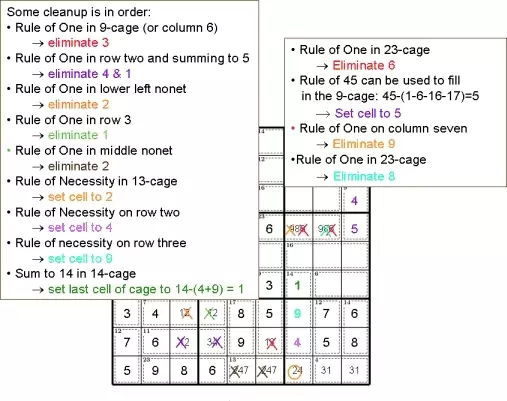
Некоторая очистка в порядке:
• Правило одного в 9 клетке (или столбец 6)
-> устранить 3
• Правило одного во втором ряду и суммирование до 5
-> исключить 4 и 1
• Правило одного в нижнем левом блоке
-> устранить 2
• Правило одного в третьем ряду
-> исключить 1
• Правило одного в среднем блоке
-> устранить 2
• Правило необходимости в 13-клетке
-> установить ячейку на 2
• Правило необходимости во втором ряду
-> установить ячейку на 4
• Правило необходимости в третьем ряду
-> ячейка до 9
• Сумма 14 в 14 клетке
-> установить последнюю ячейку клетки на 14- (4 + 9) = 1
• Правило одного в 23 клетке
-> Устранить 6
• Правило 45 можно использовать для заполнения 9 клеток: 45- (1-6-16-17) = 5
-> Установить ячейку на 5
• Правило одного в седьмом столбце
-> Устранить 9
• Правило одного в 23 клетке
-> Устранить 8

Ограниченные возможные суммы
Правило 1
Правило необходимости

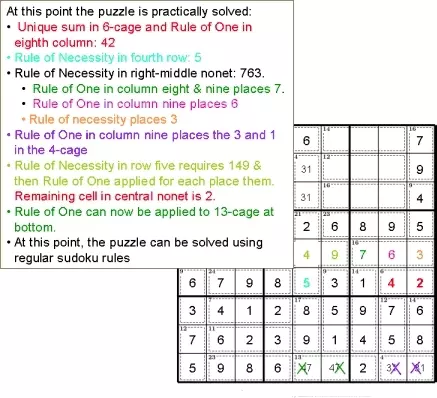
На этом эта головоломка сумдоку практически решена:
• Уникальная сумма в 6-клетке и правило одного в восьмом столбце: 42
• Правило необходимости в четвертом ряду: 5
• Правило необходимости в правом среднем ноне: 763.
• Правило одного в столбце восемь и девять мест 7.
• Правило одного в девятом столбце 6
• Правило необходимости - 3 места
• Правило одного в девятом столбце помещает 3 и 1 в клетку из 4
• Правило необходимости в пятом ряду требует 149, а затем применяется Правило одного для каждого места.

В центральном блоке осталось 2 ячейки.
• Правило одного теперь можно применить к 13 клетке внизу.
• На этом этапе головоломку можно решить, используя обычные правила судоку.

Правило необходимости
Правило 1

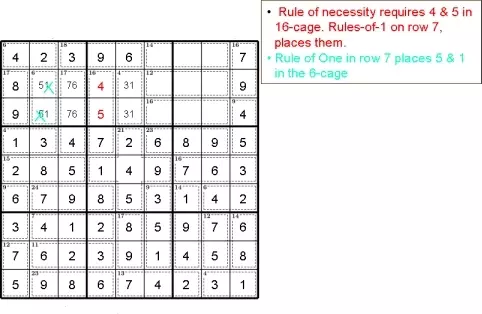
• Правило необходимости требует 4 и 5 в 16 клетках. Правило-1 в строке 7, размещает их.
• Правило одного в ряду 7 помещает 5 и 1 в клетку из 6

Рассмотрим более сложный пример, основанный на Сумдоку №24

Многие присылают мне письма или пишут комментарии, в которых говорится, что единственный подход к решению некоторых онлайн Сумдоку - это метод проб и ошибок. Учитывая объем писем, я публикую первоначальный подход до этой головоломки.

Начните с использования Правила 45 в двух столбцах слева, что даст: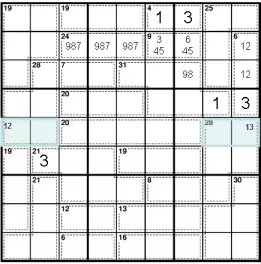

3 в r4c2
1 в r8c6
Уникальная сумма в 4 клетках в сочетании с уникальной суммой в 6 клетках

3 в r9c7
1 в r9c6
3 в r6c9
и остаток 6-клетки (1 + 2) в r7c9 и r8c9.
Заполните уникальную сумму 24 клеток в строке 8.

Единственные возможности для 9 клеток в 8 ряду теперь 4 + 5 и 3 + 6.

Теперь используйте правило 45 в нижних 5 рядах, чтобы определить значение 2 ячеек (синего цвета) в верхней части 28 клетки справа от головоломки. Исходя из этого, вычислите значение 2 ячеек внизу 28-й клетки слева, также отмеченных синим цветом.


Единственные возможные совместимые суммы в двух синих клетках: 8 + 4 и 7 + 5 слева и 7 + 6 и 9 + 4 справа.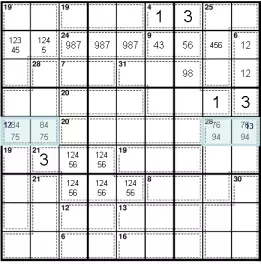

Единственно возможная сумма в клетке из 21 в третьем и четвертом рядах составляет 3 + 1 + 2 + 4 + 5 + 6.

Из правила 45 в правом верхнем углу блока мы видим, что сумма в крайнем левом столбце 3 должна быть равна 17. Это означает, что r7c7 должно быть 8 или 9. (Это также означает, что r8c7 не может быть 4.)

Правило необходимости позволяет нам определить, что r8c8 должно быть 456. Таким образом, две крайние правые ячейки восьмой строки - это 12345 и 1245 соответственно.


Сумма верхней части 28-клетки (обозначена зеленым) должна быть 16. Мы знаем, что эта сумма не может содержать ни 3, ни 1.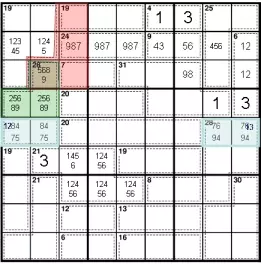

Он не может содержать 3 из-за r4c2.
Он не может содержать 1 из-за 1 в r6c8 и того факта, что сумма красной области должна быть равна 26 (из-за правила 45). Красная область состоит из 4 ячеек, и нет суммы из 4 ячеек, равной 26 с единицей.
Мы также знаем, что сумма не может содержать и (7 и 8), или (4 и 5), или (8 и 5), или (7 и 4). Если бы он содержал одну из этих пар, то было бы невозможно заполнить синюю часть 28-клетки. Это оставляет 259 и 268 как единственно возможные суммы для верхней части 28-й клетки. Наконец, мы знаем, что 2 должны быть в r6. Если бы 2 было в r7c2, это потребовало бы, чтобы красная область состояла из 9872, однако это означало бы, что r7c3 в 7-клетке будет иметь значение больше 6; что невозможно.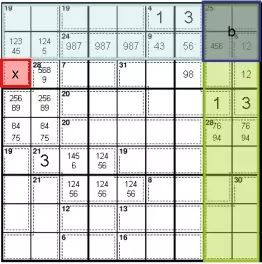


Теперь можно использовать форму Правила перекрытия (впервые предложенную Жаном-Кристофом Годаром) для сбора информации о верхнем правом и верхнем левом блоках. В этом случае мы складываем клетки, содержащиеся в синей и зеленой областях, чтобы получить 165. Из простых математических расчетов мы видим, что область b (темно-синяя) подсчитывается один раз путем сложения суммы клеток и считается дважды, если мы просто добавляем вверх два ряда и два столбца. То есть:

165-х + b = 180.
Где 165 - это сумма клеток, x - дополнительная ячейка, включенная в сумму клеток, которая не включена в синие строки, b - площадь, подсчитываемая дважды путем суммирования отдельных строк и столбцов, а 180 - это площадь сумма строк и столбцов.

Итак, b = 15 + x. Поскольку минимальное значение b может быть равно 17 (4 + 1 + 7 + 5), а максимальное - 24 (6 + 2 + 9 + 7), мы можем видеть, что x должен быть между 2 и 9. Если вы проверите r7, это означает, что единственная ячейка, которая может содержать 1, - это r7c9.


Правило 45 теперь позволяет нам сделать вывод, что x + y = 12.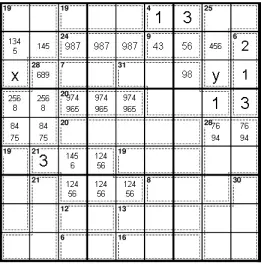

Теперь мы можем определить, что r7c2 не может быть 5, поскольку 7-клетка на r7 должна быть либо 5 + 2, либо 3 + 4. Однако, если r7c2 равно 5, то x + y должен использовать либо 3, либо 4.

Теперь мы можем осмотреть 20-клетку на r6. Из-за 3 в r6c9 единственными действительными суммами являются 875, 974 и 965. Однако 875 не является законным, поскольку:

r6c3 не может быть 8. Если r6c3 = 8, тогда r7c2 = 8 (по Правилу необходимости на 28-клетке), что означает, что r7c7 должно быть 9. Но тогда в r6 нет места для 9.
r6c3 не может быть ни 5, ни 7. Если бы это было так, то 28-клетка была бы невозможна.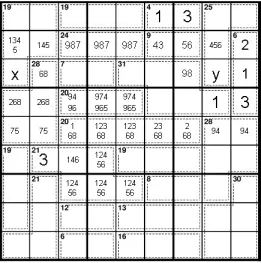


Мы можем исключить возможность 259 в верхней части 28-клетки, потому что 25 в r6c12 потребует 974 в 20-клетке на r6, оставляя 68 в r6c67. Однако 9 в r7c2 превращает r7c7 в 8, поэтому в клетке с 31 будет две восьмерки.

Это, в свою очередь, позволяет нам зафиксировать сумму r5c12 равной 7 + 5.

Затем мы можем исключить 7 и 5 из остальных ячеек в этом блоке.

Мы также можем ввести возможные значения для остальной части r5.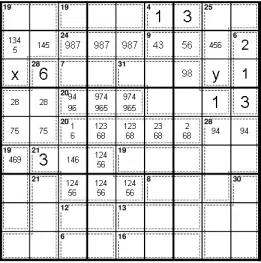


Теперь мы можем исключить 8 в r7c2, так как это делает невозможным 31 клетку. Если r7c2 - 8, то r7c567 должно быть 6 + 9 + (3 или 4). Но r6c678 может быть только 5 + 8 + 1; что не может в сумме равняться 31.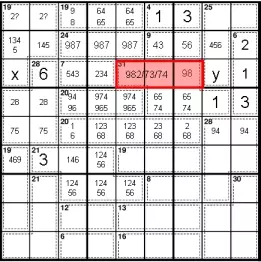


Правило необходимости делает r6c67 = 65 или 74. Таким образом, красная область должна равняться 19. Единственные допустимые суммы для красной области - 982, 973 и 874. Это означает, что r7c56 должно иметь одну из 987.

Использование Правила K в верхнем среднем блоке позволяет нам исключить все случаи использования 987 за пределами 24-клетки на r8 и красной области. Таким образом, 19-клетка на r9 должна быть 964 или 865.

Правило необходимости требует 2 в r9c12.

Таким образом, 7-клетка на r7 равна 5 + 2, 3 + 4 или 4 + 3.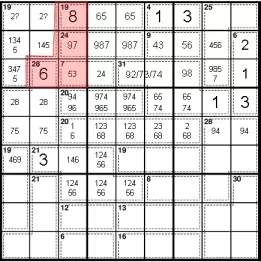


По правилу необходимости сделайте 19-клетку на r9 равной 865. (Так как других 5 нет в верхнем среднем блоке).

Красная область в верхнем левом блоке должна составлять 26 по правилу 45. Таким образом, сумма r78c3 должна быть равна 12. Это исключает 4 из r7c3.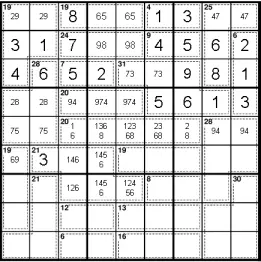


Чтобы добиться прогресса, нам теперь нужна некоторая информация из нижней части головоломки. Первое, что нужно искать, - это максимально ограниченная клетка. Это будет 30-я клетка в правом нижнем углу. Он не может содержать ни 1, ни 4. (В нем не может быть 4, поскольку 28-я клетка над ним имеет 4, а в r789c7 нет 4. Таким образом, у c89 уже есть свои четверки.) Каждая сумма, которая составляет 30 без 1 или 4 дает 9! Таким образом, r789c89 не может иметь 9! Это означает, что r7c7 - 9.

В настоящее время можно добиться значительного прогресса.

У 19-клетки в c1 есть только одна возможная сумма: 658.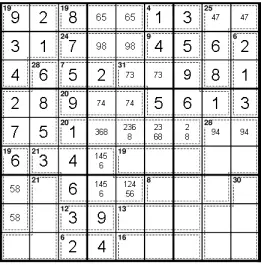

Число 58 в r23c1 позволяет нам исправить остальные ячейки в верхнем левом блоке.

6 в r4c1 также очищает столбец 3 в этом блоке.

Остается только 236 для r123c3. Однако из-за ценности клеток мы можем сразу их разместить.

Теперь остальная часть головоломки встает на свои места.