Следующая Японские кроссворды, правила игры Nonograms  Предыдущая
Предыдущая
Понравился материал? Будем благодарны за репосты.
 Предыдущая
Предыдущая
Большинство людей, похоже, не нуждаются в большой инструкции о том, как решать головоломки Японские кроссворды (с разбивкой по числу или нонограммы, griddlers, hanjie, picross или что-то еще, как вам нравится их называть). Базовый метод решения легко продемонстрирован в простом примере, например, на первой странице этого сайта. Я ожидаю, что наиболее разумно умные люди могут понять это, даже не будучи показанными. И эта базовая техника решения действительно довольно мощная и может быть использована для решения большинства головоломок. Однако есть некоторые случаи, когда для решения головоломки требуются несколько более сложные логические трюки.
Эта страница призвана дать некоторые идеи о причудливых методах решения нонограмм, а также установить некоторую терминологию для обсуждения способов решения на форумах на этом сайте.
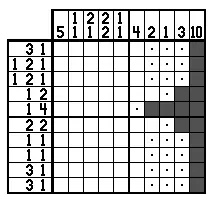
«Линейное решение» - это когда вы работаете с одной строкой или одной колонкой за раз. Иногда это просто и прямо, как в случае ниже, где мы знаем, что ячейки с надписью «A» должны быть черными:

Пример 1.
Иногда требуется немного подумать о разных случаях, например, в случае ниже, где одиночная ячейка «B» должна быть черной:

Пример 2.
И иногда есть вещи, которые довольно чертовы трудно обнаружить, например, тот факт, что ячейка «C» в строке ниже должна быть белой:

Пример 3.
Но хотя решение линии не всегда «просто» в смысле простоты, оно, по крайней мере, всегда предполагает просмотр только одной строки или столбца за раз.
Кстати, компьютерные программы, написанные для решения головоломок с разбивкой по числу, поддерживают линию линии. Это то, что любит компьютер, - глядя на одну небольшую часть проблемы одновременно и надеясь, что из этого выйдет общее решение. Пазлы, разрешаемые только линейным решением, почти всегда легко разрешаются компьютерами. Это в тех случаях, когда вы должны смотреть на большую часть загадки, чтобы понять, что люди действительно могут развернуть компьютерные программы.
Вот симметричная головоломка (предупреждение компульсивным решателям: это не похоже на что-либо, когда оно разрешено. Это всего лишь пример симметрии.):

Пример 4.
Линейное решение не дает вам нигде в этой головоломке.
Но головоломка симметрична, в том смысле, что она точно такая же, как зеркальное отражение. Каждый горизонтальный ключ обратим. «1 1» назад - «1 1». Верхний ключ в столбце 1 такой же, как в столбце 4, а верхний ключ в столбце 2 совпадает с столбцом 3.
Очевидно, если вы нашли решение этой головоломки и отразили решение вокруг вертикальной оси, то это зеркальное изображение также было бы решением головоломки. Если есть только одно решение, то мы знаем, что решение должно быть симметричным. Знать, что решение является симметричным, является действительно большим ключом.
К сожалению, на этом веб-сайте, по крайней мере, вы никогда не можете быть уверены, что головоломка действительно имеет только одно решение, и, не зная, что решение проблемы с использованием симметрии - это немного обманщик. Обычно мы не рассматриваем головоломку «логически разрешимой», если ее можно решить только симметрией. Исключением является то, что если автор головоломки помещает некоторую информацию в заголовок головоломки типа «[имеет только одно решение]», то вполне законно использовать симметрию для решения головоломки, потому что эта информация была предоставлена для использования в качестве части головоломки.
Как только вы узнаете, что решение головоломки выше симметрично, тривиально его решить. Во-первых, если какой-либо боковой ключ имеет в нем нечетное количество идентификационных номеров (например, строки «2»), то центральные столбцы должны быть черными. И если у него есть четное число номеров ключей, то центральные столбцы должны быть белыми. (В этом случае у нас есть два центральных столбца, но если головоломка имеет нечетное число столбцов, у нас будет только один.) Этого достаточно для решения большинства симметричных головоломок.
Конечно, существуют и другие формы симметрии. Головоломка может иметь вертикальную симметрию или диагональную симметрию, или вращательную симметрию (хотя она должна быть квадратной для любой из двух или двух последних).
Хотя решение по симметрии является своего рода обманом, это, конечно, не случай, когда он смотрит только на одну строку за раз. Вы действительно должны смотреть на всю головоломку, чтобы обнаружить симметрию.
Наиболее очевидным видом логики, которая включает в себя одновременное рассмотрение строк и столбцов, является «цветовая логика». Это происходит в многоцветных головоломках, когда подсказка строки сообщает вам, что ячейка должна быть либо цветом A, либо цветом B, в то время как в подсказке столбца говорится, что это должен быть либо цвет B, либо цвет C, поэтому мы можем заключить, что это должен быть цвет B.
Вот простой пример:
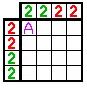
Пример 5.
Опять же, линейная логика не работает, но совершенно очевидно, что ячейка «А» должна быть белой. В конце концов, подсказка в строке говорит, что она может быть только красной или белой, а подсказка в столбце говорит, что она может быть только зеленой или белой, поэтому она должна быть белой.
Вот более сложный пример:
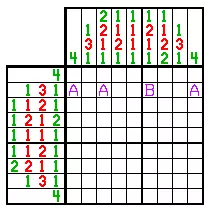
Пример 6.
Опять же, решение линии не дает нам нигде, и мы проигнорируем вращательную симметрию головоломки (что сложно понять и обмануть).
Производственная линия рассуждений, однако, заключается в том, чтобы спросить, какие ячейки во втором ряду могут быть красными. Посмотрев на главные подсказки, мы видим, что ячейки, отмеченные «А», не могут быть красными. Они могут быть зелеными или белыми, но не красными. Но если это так, то ячейка «B» должна быть красной и может быть отмечена красным цветом, потому что каждое место, которое красные три могут включать в себя эту ячейку. Та же логика может применяться на трех других сторонах головоломки, и как только вы это сделаете, остальная часть головоломки легко решить с помощью решения линии.
Трюк с цветовой логикой запоминает, какие цвета могут быть у каждой ячейки. Некоторые компьютерные программы, такие как «контролер», используемые на этом сайте, сохраняют список возможных цветов для каждой ячейки. Если вы это сделаете, то все вышеописанные головоломки легко решить простым обычным решением (хотя алгоритм решения строк становится немного сложнее). Возможно, вы могли бы придумать какую-то систему обозначений, которая позволила бы вам делать то же самое на бумаге, но я сомневаюсь, что это действительно было бы полезно. На практике это просто вопрос, чтобы понять это в вашей голове. Трудно, но я не думаю, что пример 6 действительно сложнее, чем, скажем, пример 3.
«Граничная логика» (или «Edge logic») - это логический трюк, часто полезный по краям головоломки. Головоломка № 23 на этом сайте была разработана в качестве примера такого рода вещей. Это выглядит так:
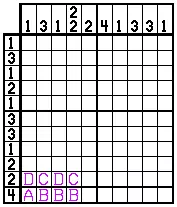
Пример 7а
Трудно представить себе головоломку, менее доступную для решения линии. Опытные решатели сразу заметят одну многообещающую функцию: вдоль нижнего края есть довольно большое число («4») с небольшими номерами («2») в следующей строке вверх.
Трюк в таких случаях состоит в том, чтобы рассмотреть эти две строки вместе. Поскольку строка «4» находится прямо на краю головоломки, легко понять, каковы последствия, если «4» находится в разных местах и проверить, соответствуют ли эти последствия строке «2». Поэтому мы просто мысленно пробуем «4» в разных позициях. Мы могли бы начать с предположения, что ячейка «А» была черной. Очевидно, это означало бы, что все ячейки с надписью «B» также должны быть черными. Посмотрев на подсказки столбца, мы видим, что две ячейки с пометкой «C» также должны быть черными. Хотя ячейки с надписью «D» должны быть белыми. Но это делает невозможным образец черных и белых в этой строке. В этой строке может быть только два. Таким образом, это означает, что «А» не может быть черным и должен быть белым.
Как только вы получите представление об этом, довольно легко увидеть, что большинство мест, где вы могли бы разместить четыре в нижнем ряду, создавали бы невозможный шаблон во второй строке снизу. В этой головоломке фактически есть только одно место, которое может быть, это положение, показанное ниже. В любом другом положении он либо дал бы трех черных во втором ряду, либо двух чернокожих с белым между ними.
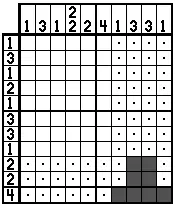
Пример 7б
Если мы хотим продолжить решение этой головоломки, мы снова применим тот же трюк. На этот раз мы будем работать с 4 в столбце 6. Хотя в этом случае мы не работаем с внешним краем головоломки, мы все еще делаем одну и ту же основную вещь на краю неизвестной области.
Логика края полезна во множестве головоломок, но обычно это не работает так же хорошо, как в примере 7. Часто вы обнаружите, что существует несколько разных мест, где может существовать краевой блок. Но этого все равно может хватить, чтобы вы могли расставить несколько ячеек (особенно в углах), и может быть, что все возможные положения перекрываются на нескольких ячейках, которые вы можете нарисовать черным.
Существует множество вариантов краевой логики. Иногда первая строка внутрь может оказаться бесполезной, но вторая строка внутри будет более полезна. Иногда вы даже можете применить его к размещению блока в первой строке вовнутрь, проверяя согласованность со второй строкой внутрь.
Хорошей первой загадкой, чтобы попробовать логику края, является # 6336.
Другой шаблон, который часто встречается, - это «улыбка». Мы называем это тем, что самая распространенная форма, в которой он появляется, - головоломка в форме улыбки ниже:
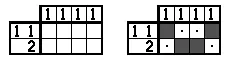
Пример 8.
Решение, показанное справа, уникально, но ни один из описанных выше методов не позволяет нам его решить (ну, симметрия, но мы не хотим использовать симметрию).
Ключом к нему являются все те, что указаны в подсказках столбцов. Мы знаем, что в каждом столбце может быть только один черный цвет, поэтому мы знаем, что горизонтальные блоки 1 и 2 никогда не могут перекрывать друг друга. Поскольку 1 не могут быть рядом друг с другом (потому что нам нужно пустое пространство между ними), блоки из двух строк должны чередоваться. Они должны идти 1,2,1.
То же самое рассуждение применимо к головоломке ниже, с решением, которое больше похоже на змею, чем на улыбку:

Пример 9.
Обычно головоломки не начинаются с так много столбцов, содержащих только один. Это скорее своего рода ситуация, которая иногда развивается в головоломке, которая почти завершена, где в столбцах было много других номеров ключей, но они уже были размещены. Логика улыбки - это то, что обычно используется в конце процесса решения, в отличие от краевой логики, которая может применяться в любой точке. (Но для исключения из этого правила см. Гламур # 6542).
Еще одна распространенная вариация логики улыбки встречается в таких ситуациях, как головоломка ниже:
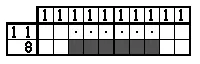
Пример 10.
Эта головоломка уже частично решена с использованием классического решения линий, но решение линии не дает нам дальнейших результатов. Но восемь нераскрытых квадратов действительно находятся в той же ситуации, что и базовый шаблон улыбки в примере 8. Для решения этой проблемы могут применяться те же аргументы.
Пример ниже похож на тот, который я когда-то использовал, когда я застрял. У меня нет по-настоящему умного имени, но на данный момент я называю это «двухсторонней логикой». Это было решено, поскольку решение по линии вас возьмет. Что не столь очевидно, так это то, что все ячейки с надписью «A» должны быть белыми.
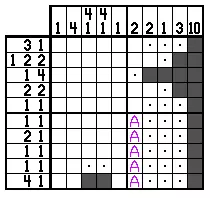
Пример 11.
Эти рассуждения идут так. Очевидно, что блок «2» в столбце 7 может находиться только в одном из двух положений. Это говорит нам о столбце 6: либо ячейке непосредственно над пунктирной ячейкой, либо непосредственно под пунктирной ячейкой должно быть черным. Таким образом, «2» в этом столбце может находиться только в одной из двух позиций, которые не содержат никаких ячеек «А», поэтому мы можем их расставить. Оттуда остальная часть головоломки легко решается. (Фактически, пример 11 - это не все, что искусно спроектировано, потому что оно также может быть решено с помощью краевой логики).
Итак, основная идея здесь - искать места, где вы знаете, что одна из двух ячеек должна быть черной. Для каждого случая подумайте всего лишь о переезде или о двух, чтобы увидеть, какие другие ячейки вы могли бы установить в этом случае. Если в обоих случаях любые ячейки устанавливаются одинаково, вы можете их пометить.
Несколько другой пример того же трюка показан ниже. Использование двухсторонней логики в двух открытых ячейках в столбце семь позволяет вам установить ровно одну ячейку, которая позволяет решить оставшуюся часть головоломки:

Пример 12.
Ты нашел это? Это ячейка в четвертом ряду и шестой столбец, и она должна быть белой. Если «2» в столбце семь находится в верхнем положении, тогда вся остальная часть четвертой строки должна быть белой. Если «2» находится в нижнем положении, верхняя половина столбца шесть должна быть белой. В любом случае, одна ячейка должна быть белой.
Опять же, случается, что эта головоломка также может быть решена с помощью краевой логики. Трудно справиться с маленькими головоломками, которые могут быть решены только двунаправленной логикой.
Иногда интересные вещи могут быть достигнуты путем суммирования количества ячеек, которые необходимо установить в определенном регионе. Вот головоломка, надуманная, чтобы продемонстрировать этот трюк:
Иногда интересные вещи могут быть достигнуты путем суммирования количества ячеек, которые необходимо установить в определенном регионе. Вот головоломка, надуманная, чтобы продемонстрировать этот трюк:
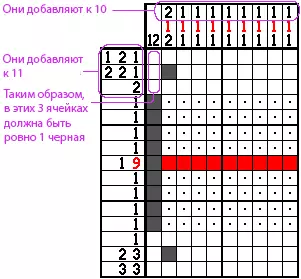
Пример 13.
Мы использовали простое решение линии, чтобы заполнить много места, но у нас есть нераскрытые области наверху, а внизу все еще предстоит выяснить. Следующее, что мы, естественно, попытаемся завершить эту головоломку, было бы краевой логикой на 12 в первой колонке, но это ничего не дает нам.
Но есть простой трюк, который расскажет нам, где именно должно быть 12. Во-первых, используйте подсказки строк, чтобы добавить количество ячеек, которые необходимы в трех верхних строках. Первая строка равна 1 + 2 + 1 = 4, вторая - 2 + 2 + 1 = 5, а третья - всего 2, поэтому общее число равно 4 + 5 + 2 = 11. Нам нужно в общей сложности 11 черных клеток в трех верхних рядах головоломки.
Теперь, если мы посмотрим на подсказки столбца, мы можем использовать их для определения количества ячеек в трех верхних строках для каждого столбца, кроме первого столбца. Столбец 2 должен иметь 2 ячейки, а остальные восемь столбцов должны иметь по одному, в общей сложности 10.
Итак, поскольку подсказки строки говорят нам, что в верхней части должно быть 11 ячеек, и, поскольку мы знаем, что в столбцах с 2 по 10 есть 10, в первых трех строках столбца 1 должна быть ровно одна черная ячейка. говорит нам точно, где должно быть 12 в столбце 1, а остальная часть головоломки тривиальна для решения.
Я только когда-либо использовал этот трюк в нескольких головоломках, но он отличный, когда он работает.
Очевидно, что это не исчерпывающий список всех фантастических логических трюков, которые полезны при решении Японских кроссвордов. Иногда вам нужно изобрести новую ткань из цельной ткани, чтобы решить загадку. Но эй, это весело, не так ли?
Конечно, некоторые люди предпочитают решать кроссворды просто догадываясь, будет ли ситуация жесткой. Если это вас радует, то со мной все в порядке.
Эта страница призвана дать некоторые идеи о причудливых методах решения нонограмм, а также установить некоторую терминологию для обсуждения способов решения на форумах на этом сайте.
Линейное решение
«Линейное решение» - это когда вы работаете с одной строкой или одной колонкой за раз. Иногда это просто и прямо, как в случае ниже, где мы знаем, что ячейки с надписью «A» должны быть черными:

Пример 1.
Иногда требуется немного подумать о разных случаях, например, в случае ниже, где одиночная ячейка «B» должна быть черной:

Пример 2.
И иногда есть вещи, которые довольно чертовы трудно обнаружить, например, тот факт, что ячейка «C» в строке ниже должна быть белой:

Пример 3.
Но хотя решение линии не всегда «просто» в смысле простоты, оно, по крайней мере, всегда предполагает просмотр только одной строки или столбца за раз.
Кстати, компьютерные программы, написанные для решения головоломок с разбивкой по числу, поддерживают линию линии. Это то, что любит компьютер, - глядя на одну небольшую часть проблемы одновременно и надеясь, что из этого выйдет общее решение. Пазлы, разрешаемые только линейным решением, почти всегда легко разрешаются компьютерами. Это в тех случаях, когда вы должны смотреть на большую часть загадки, чтобы понять, что люди действительно могут развернуть компьютерные программы.
Симметричность
Вот симметричная головоломка (предупреждение компульсивным решателям: это не похоже на что-либо, когда оно разрешено. Это всего лишь пример симметрии.):

Пример 4.
Линейное решение не дает вам нигде в этой головоломке.
Но головоломка симметрична, в том смысле, что она точно такая же, как зеркальное отражение. Каждый горизонтальный ключ обратим. «1 1» назад - «1 1». Верхний ключ в столбце 1 такой же, как в столбце 4, а верхний ключ в столбце 2 совпадает с столбцом 3.
Очевидно, если вы нашли решение этой головоломки и отразили решение вокруг вертикальной оси, то это зеркальное изображение также было бы решением головоломки. Если есть только одно решение, то мы знаем, что решение должно быть симметричным. Знать, что решение является симметричным, является действительно большим ключом.
К сожалению, на этом веб-сайте, по крайней мере, вы никогда не можете быть уверены, что головоломка действительно имеет только одно решение, и, не зная, что решение проблемы с использованием симметрии - это немного обманщик. Обычно мы не рассматриваем головоломку «логически разрешимой», если ее можно решить только симметрией. Исключением является то, что если автор головоломки помещает некоторую информацию в заголовок головоломки типа «[имеет только одно решение]», то вполне законно использовать симметрию для решения головоломки, потому что эта информация была предоставлена для использования в качестве части головоломки.
Как только вы узнаете, что решение головоломки выше симметрично, тривиально его решить. Во-первых, если какой-либо боковой ключ имеет в нем нечетное количество идентификационных номеров (например, строки «2»), то центральные столбцы должны быть черными. И если у него есть четное число номеров ключей, то центральные столбцы должны быть белыми. (В этом случае у нас есть два центральных столбца, но если головоломка имеет нечетное число столбцов, у нас будет только один.) Этого достаточно для решения большинства симметричных головоломок.
Конечно, существуют и другие формы симметрии. Головоломка может иметь вертикальную симметрию или диагональную симметрию, или вращательную симметрию (хотя она должна быть квадратной для любой из двух или двух последних).
Хотя решение по симметрии является своего рода обманом, это, конечно, не случай, когда он смотрит только на одну строку за раз. Вы действительно должны смотреть на всю головоломку, чтобы обнаружить симметрию.
Цветовая логика
Наиболее очевидным видом логики, которая включает в себя одновременное рассмотрение строк и столбцов, является «цветовая логика». Это происходит в многоцветных головоломках, когда подсказка строки сообщает вам, что ячейка должна быть либо цветом A, либо цветом B, в то время как в подсказке столбца говорится, что это должен быть либо цвет B, либо цвет C, поэтому мы можем заключить, что это должен быть цвет B.
Вот простой пример:

Пример 5.
Опять же, линейная логика не работает, но совершенно очевидно, что ячейка «А» должна быть белой. В конце концов, подсказка в строке говорит, что она может быть только красной или белой, а подсказка в столбце говорит, что она может быть только зеленой или белой, поэтому она должна быть белой.
Вот более сложный пример:

Пример 6.
Опять же, решение линии не дает нам нигде, и мы проигнорируем вращательную симметрию головоломки (что сложно понять и обмануть).
Производственная линия рассуждений, однако, заключается в том, чтобы спросить, какие ячейки во втором ряду могут быть красными. Посмотрев на главные подсказки, мы видим, что ячейки, отмеченные «А», не могут быть красными. Они могут быть зелеными или белыми, но не красными. Но если это так, то ячейка «B» должна быть красной и может быть отмечена красным цветом, потому что каждое место, которое красные три могут включать в себя эту ячейку. Та же логика может применяться на трех других сторонах головоломки, и как только вы это сделаете, остальная часть головоломки легко решить с помощью решения линии.
Трюк с цветовой логикой запоминает, какие цвета могут быть у каждой ячейки. Некоторые компьютерные программы, такие как «контролер», используемые на этом сайте, сохраняют список возможных цветов для каждой ячейки. Если вы это сделаете, то все вышеописанные головоломки легко решить простым обычным решением (хотя алгоритм решения строк становится немного сложнее). Возможно, вы могли бы придумать какую-то систему обозначений, которая позволила бы вам делать то же самое на бумаге, но я сомневаюсь, что это действительно было бы полезно. На практике это просто вопрос, чтобы понять это в вашей голове. Трудно, но я не думаю, что пример 6 действительно сложнее, чем, скажем, пример 3.
Граничная логика
«Граничная логика» (или «Edge logic») - это логический трюк, часто полезный по краям головоломки. Головоломка № 23 на этом сайте была разработана в качестве примера такого рода вещей. Это выглядит так:

Пример 7а
Трудно представить себе головоломку, менее доступную для решения линии. Опытные решатели сразу заметят одну многообещающую функцию: вдоль нижнего края есть довольно большое число («4») с небольшими номерами («2») в следующей строке вверх.
Трюк в таких случаях состоит в том, чтобы рассмотреть эти две строки вместе. Поскольку строка «4» находится прямо на краю головоломки, легко понять, каковы последствия, если «4» находится в разных местах и проверить, соответствуют ли эти последствия строке «2». Поэтому мы просто мысленно пробуем «4» в разных позициях. Мы могли бы начать с предположения, что ячейка «А» была черной. Очевидно, это означало бы, что все ячейки с надписью «B» также должны быть черными. Посмотрев на подсказки столбца, мы видим, что две ячейки с пометкой «C» также должны быть черными. Хотя ячейки с надписью «D» должны быть белыми. Но это делает невозможным образец черных и белых в этой строке. В этой строке может быть только два. Таким образом, это означает, что «А» не может быть черным и должен быть белым.
Как только вы получите представление об этом, довольно легко увидеть, что большинство мест, где вы могли бы разместить четыре в нижнем ряду, создавали бы невозможный шаблон во второй строке снизу. В этой головоломке фактически есть только одно место, которое может быть, это положение, показанное ниже. В любом другом положении он либо дал бы трех черных во втором ряду, либо двух чернокожих с белым между ними.

Пример 7б
Если мы хотим продолжить решение этой головоломки, мы снова применим тот же трюк. На этот раз мы будем работать с 4 в столбце 6. Хотя в этом случае мы не работаем с внешним краем головоломки, мы все еще делаем одну и ту же основную вещь на краю неизвестной области.
Логика края полезна во множестве головоломок, но обычно это не работает так же хорошо, как в примере 7. Часто вы обнаружите, что существует несколько разных мест, где может существовать краевой блок. Но этого все равно может хватить, чтобы вы могли расставить несколько ячеек (особенно в углах), и может быть, что все возможные положения перекрываются на нескольких ячейках, которые вы можете нарисовать черным.
Существует множество вариантов краевой логики. Иногда первая строка внутрь может оказаться бесполезной, но вторая строка внутри будет более полезна. Иногда вы даже можете применить его к размещению блока в первой строке вовнутрь, проверяя согласованность со второй строкой внутрь.
Хорошей первой загадкой, чтобы попробовать логику края, является # 6336.
Улыбка логика
Другой шаблон, который часто встречается, - это «улыбка». Мы называем это тем, что самая распространенная форма, в которой он появляется, - головоломка в форме улыбки ниже:

Пример 8.
Решение, показанное справа, уникально, но ни один из описанных выше методов не позволяет нам его решить (ну, симметрия, но мы не хотим использовать симметрию).
Ключом к нему являются все те, что указаны в подсказках столбцов. Мы знаем, что в каждом столбце может быть только один черный цвет, поэтому мы знаем, что горизонтальные блоки 1 и 2 никогда не могут перекрывать друг друга. Поскольку 1 не могут быть рядом друг с другом (потому что нам нужно пустое пространство между ними), блоки из двух строк должны чередоваться. Они должны идти 1,2,1.
То же самое рассуждение применимо к головоломке ниже, с решением, которое больше похоже на змею, чем на улыбку:

Пример 9.
Обычно головоломки не начинаются с так много столбцов, содержащих только один. Это скорее своего рода ситуация, которая иногда развивается в головоломке, которая почти завершена, где в столбцах было много других номеров ключей, но они уже были размещены. Логика улыбки - это то, что обычно используется в конце процесса решения, в отличие от краевой логики, которая может применяться в любой точке. (Но для исключения из этого правила см. Гламур # 6542).
Еще одна распространенная вариация логики улыбки встречается в таких ситуациях, как головоломка ниже:

Пример 10.
Эта головоломка уже частично решена с использованием классического решения линий, но решение линии не дает нам дальнейших результатов. Но восемь нераскрытых квадратов действительно находятся в той же ситуации, что и базовый шаблон улыбки в примере 8. Для решения этой проблемы могут применяться те же аргументы.
Двусторонняя логика
Пример ниже похож на тот, который я когда-то использовал, когда я застрял. У меня нет по-настоящему умного имени, но на данный момент я называю это «двухсторонней логикой». Это было решено, поскольку решение по линии вас возьмет. Что не столь очевидно, так это то, что все ячейки с надписью «A» должны быть белыми.

Пример 11.
Эти рассуждения идут так. Очевидно, что блок «2» в столбце 7 может находиться только в одном из двух положений. Это говорит нам о столбце 6: либо ячейке непосредственно над пунктирной ячейкой, либо непосредственно под пунктирной ячейкой должно быть черным. Таким образом, «2» в этом столбце может находиться только в одной из двух позиций, которые не содержат никаких ячеек «А», поэтому мы можем их расставить. Оттуда остальная часть головоломки легко решается. (Фактически, пример 11 - это не все, что искусно спроектировано, потому что оно также может быть решено с помощью краевой логики).
Итак, основная идея здесь - искать места, где вы знаете, что одна из двух ячеек должна быть черной. Для каждого случая подумайте всего лишь о переезде или о двух, чтобы увидеть, какие другие ячейки вы могли бы установить в этом случае. Если в обоих случаях любые ячейки устанавливаются одинаково, вы можете их пометить.
Несколько другой пример того же трюка показан ниже. Использование двухсторонней логики в двух открытых ячейках в столбце семь позволяет вам установить ровно одну ячейку, которая позволяет решить оставшуюся часть головоломки:

Пример 12.
Ты нашел это? Это ячейка в четвертом ряду и шестой столбец, и она должна быть белой. Если «2» в столбце семь находится в верхнем положении, тогда вся остальная часть четвертой строки должна быть белой. Если «2» находится в нижнем положении, верхняя половина столбца шесть должна быть белой. В любом случае, одна ячейка должна быть белой.
Опять же, случается, что эта головоломка также может быть решена с помощью краевой логики. Трудно справиться с маленькими головоломками, которые могут быть решены только двунаправленной логикой.
Подводя итоги
Иногда интересные вещи могут быть достигнуты путем суммирования количества ячеек, которые необходимо установить в определенном регионе. Вот головоломка, надуманная, чтобы продемонстрировать этот трюк:
Иногда интересные вещи могут быть достигнуты путем суммирования количества ячеек, которые необходимо установить в определенном регионе. Вот головоломка, надуманная, чтобы продемонстрировать этот трюк:

Пример 13.
Мы использовали простое решение линии, чтобы заполнить много места, но у нас есть нераскрытые области наверху, а внизу все еще предстоит выяснить. Следующее, что мы, естественно, попытаемся завершить эту головоломку, было бы краевой логикой на 12 в первой колонке, но это ничего не дает нам.
Но есть простой трюк, который расскажет нам, где именно должно быть 12. Во-первых, используйте подсказки строк, чтобы добавить количество ячеек, которые необходимы в трех верхних строках. Первая строка равна 1 + 2 + 1 = 4, вторая - 2 + 2 + 1 = 5, а третья - всего 2, поэтому общее число равно 4 + 5 + 2 = 11. Нам нужно в общей сложности 11 черных клеток в трех верхних рядах головоломки.
Теперь, если мы посмотрим на подсказки столбца, мы можем использовать их для определения количества ячеек в трех верхних строках для каждого столбца, кроме первого столбца. Столбец 2 должен иметь 2 ячейки, а остальные восемь столбцов должны иметь по одному, в общей сложности 10.
Итак, поскольку подсказки строки говорят нам, что в верхней части должно быть 11 ячеек, и, поскольку мы знаем, что в столбцах с 2 по 10 есть 10, в первых трех строках столбца 1 должна быть ровно одна черная ячейка. говорит нам точно, где должно быть 12 в столбце 1, а остальная часть головоломки тривиальна для решения.
Я только когда-либо использовал этот трюк в нескольких головоломках, но он отличный, когда он работает.
Вывод
Очевидно, что это не исчерпывающий список всех фантастических логических трюков, которые полезны при решении Японских кроссвордов. Иногда вам нужно изобрести новую ткань из цельной ткани, чтобы решить загадку. Но эй, это весело, не так ли?
Конечно, некоторые люди предпочитают решать кроссворды просто догадываясь, будет ли ситуация жесткой. Если это вас радует, то со мной все в порядке.
Понравился материал? Будем благодарны за репосты.
Комментарии:
Будьте первыми, кто прокомментирует статью!
Петро Полюхович © 2011-2024
Присоединяйтесь к нам, если вы настоящий ценитель кроссвордов!


 Войти
Войти Кроссворды
Кроссворды Головоломки
Головоломки Судоку
Судоку Английские
Английские Турецкие
Турецкие О сайте
О сайте


